Recursive least squares¶
Recursive least squares is an expanding window version of ordinary least squares. In addition to availability of regression coefficients computed recursively, the recursively computed residuals the construction of statistics to investigate parameter instability.
The RecursiveLS class allows computation of recursive residuals and computes CUSUM and CUSUM of squares statistics. Plotting these statistics along with reference lines denoting statistically significant deviations from the null hypothesis of stable parameters allows an easy visual indication of parameter stability.
Finally, the RecursiveLS model allows imposing linear restrictions on the parameter vectors, and can be constructed using the formula interface.
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from pandas_datareader.data import DataReader
np.set_printoptions(suppress=True)
Example 1: Copper¶
We first consider parameter stability in the copper dataset (description below).
[2]:
print(sm.datasets.copper.DESCRLONG)
dta = sm.datasets.copper.load_pandas().data
dta.index = pd.date_range("1951-01-01", "1975-01-01", freq="AS")
endog = dta["WORLDCONSUMPTION"]
# To the regressors in the dataset, we add a column of ones for an intercept
exog = sm.add_constant(
dta[["COPPERPRICE", "INCOMEINDEX", "ALUMPRICE", "INVENTORYINDEX"]]
)
This data describes the world copper market from 1951 through 1975. In an
example, in Gill, the outcome variable (of a 2 stage estimation) is the world
consumption of copper for the 25 years. The explanatory variables are the
world consumption of copper in 1000 metric tons, the constant dollar adjusted
price of copper, the price of a substitute, aluminum, an index of real per
capita income base 1970, an annual measure of manufacturer inventory change,
and a time trend.
/tmp/ipykernel_4461/2153377698.py:4: FutureWarning: 'AS' is deprecated and will be removed in a future version, please use 'YS' instead.
dta.index = pd.date_range("1951-01-01", "1975-01-01", freq="AS")
First, construct and fit the model, and print a summary. Although the RLS model computes the regression parameters recursively, so there are as many estimates as there are datapoints, the summary table only presents the regression parameters estimated on the entire sample; except for small effects from initialization of the recursions, these estimates are equivalent to OLS estimates.
[3]:
mod = sm.RecursiveLS(endog, exog)
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: WORLDCONSUMPTION No. Observations: 25
Model: RecursiveLS Log Likelihood -154.720
Date: Thu, 18 Apr 2024 R-squared: 0.965
Time: 09:06:03 AIC 319.441
Sample: 01-01-1951 BIC 325.535
- 01-01-1975 HQIC 321.131
Covariance Type: nonrobust Scale 117717.127
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
const -6562.3719 2378.939 -2.759 0.006 -1.12e+04 -1899.737
COPPERPRICE -13.8132 15.041 -0.918 0.358 -43.292 15.666
INCOMEINDEX 1.21e+04 763.401 15.853 0.000 1.06e+04 1.36e+04
ALUMPRICE 70.4146 32.678 2.155 0.031 6.367 134.462
INVENTORYINDEX 311.7330 2130.084 0.146 0.884 -3863.155 4486.621
===================================================================================
Ljung-Box (L1) (Q): 2.17 Jarque-Bera (JB): 1.70
Prob(Q): 0.14 Prob(JB): 0.43
Heteroskedasticity (H): 3.38 Skew: -0.67
Prob(H) (two-sided): 0.13 Kurtosis: 2.53
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
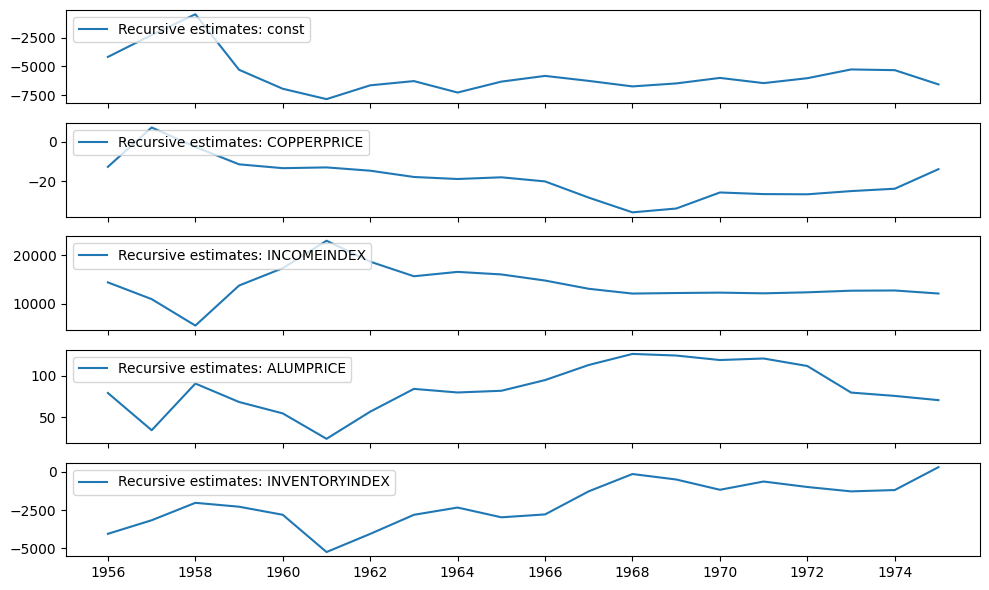
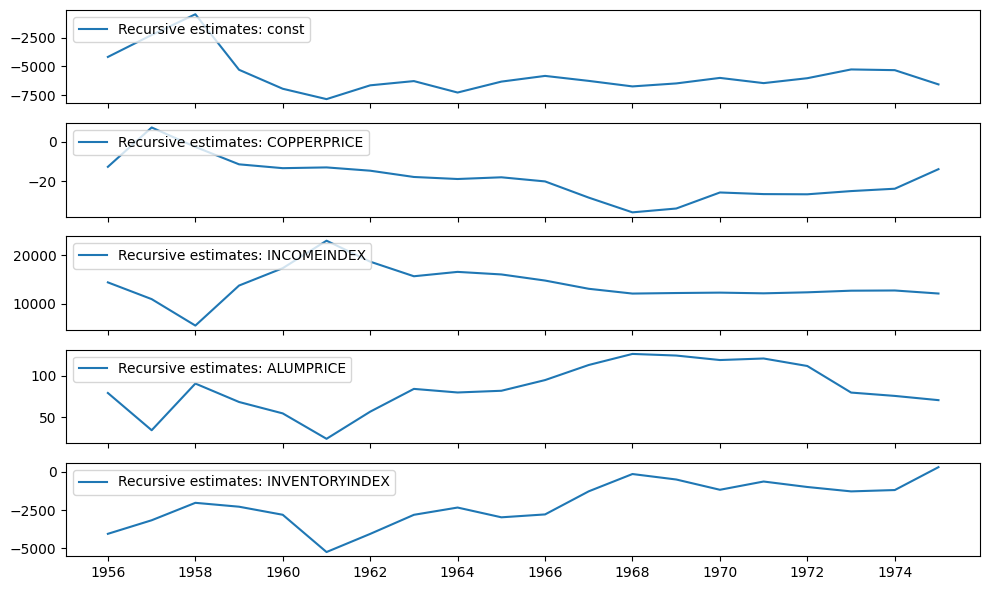
The recursive coefficients are available in the recursive_coefficients attribute. Alternatively, plots can generated using the plot_recursive_coefficient method.
[4]:
print(res.recursive_coefficients.filtered[0])
res.plot_recursive_coefficient(range(mod.k_exog), alpha=None, figsize=(10, 6))
[ 2.88890087 4.94795049 1558.41803044 1958.43326658
-51474.9578655 -4168.94974192 -2252.61351128 -446.55908507
-5288.39794736 -6942.31935786 -7846.0890355 -6643.15121393
-6274.11015558 -7272.01696292 -6319.02648554 -5822.23929148
-6256.30902754 -6737.4044603 -6477.42841448 -5995.90746904
-6450.80677813 -6022.92166487 -5258.35152753 -5320.89136363
-6562.37193573]
[4]:
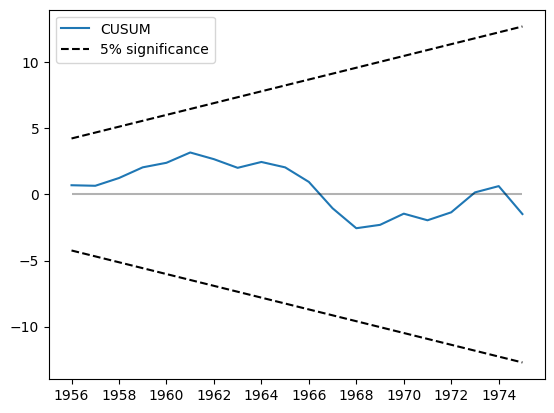
The CUSUM statistic is available in the cusum attribute, but usually it is more convenient to visually check for parameter stability using the plot_cusum method. In the plot below, the CUSUM statistic does not move outside of the 5% significance bands, so we fail to reject the null hypothesis of stable parameters at the 5% level.
[5]:
print(res.cusum)
fig = res.plot_cusum()
[ 0.69971508 0.65841244 1.24629674 2.05476032 2.39888918 3.1786198
2.67244672 2.01783215 2.46131747 2.05268638 0.95054336 -1.04505546
-2.55465286 -2.29908152 -1.45289492 -1.95353993 -1.3504662 0.15789829
0.6328653 -1.48184586]
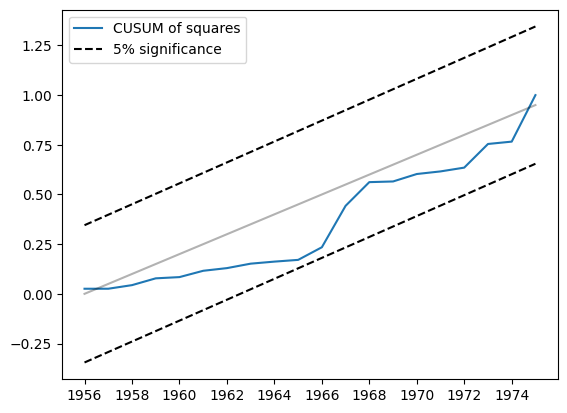
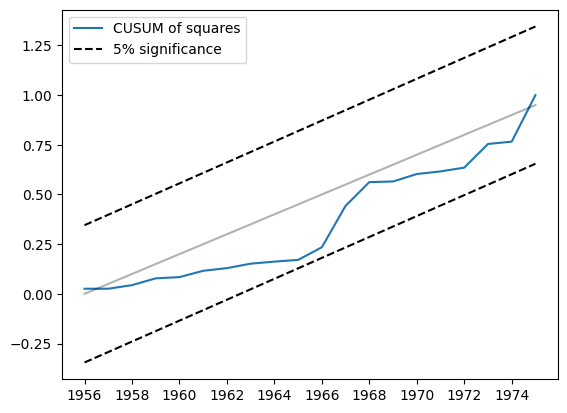
Another related statistic is the CUSUM of squares. It is available in the cusum_squares attribute, but it is similarly more convenient to check it visually, using the plot_cusum_squares method. In the plot below, the CUSUM of squares statistic does not move outside of the 5% significance bands, so we fail to reject the null hypothesis of stable parameters at the 5% level.
[6]:
res.plot_cusum_squares()
[6]:
Example 2: Quantity theory of money¶
The quantity theory of money suggests that “a given change in the rate of change in the quantity of money induces … an equal change in the rate of price inflation” (Lucas, 1980). Following Lucas, we examine the relationship between double-sided exponentially weighted moving averages of money growth and CPI inflation. Although Lucas found the relationship between these variables to be stable, more recently it appears that the relationship is unstable; see e.g. Sargent and Surico (2010).
[7]:
start = "1959-12-01"
end = "2015-01-01"
m2 = DataReader("M2SL", "fred", start=start, end=end)
cpi = DataReader("CPIAUCSL", "fred", start=start, end=end)
[8]:
def ewma(series, beta, n_window):
nobs = len(series)
scalar = (1 - beta) / (1 + beta)
ma = []
k = np.arange(n_window, 0, -1)
weights = np.r_[beta ** k, 1, beta ** k[::-1]]
for t in range(n_window, nobs - n_window):
window = series.iloc[t - n_window : t + n_window + 1].values
ma.append(scalar * np.sum(weights * window))
return pd.Series(ma, name=series.name, index=series.iloc[n_window:-n_window].index)
m2_ewma = ewma(np.log(m2["M2SL"].resample("QS").mean()).diff().iloc[1:], 0.95, 10 * 4)
cpi_ewma = ewma(
np.log(cpi["CPIAUCSL"].resample("QS").mean()).diff().iloc[1:], 0.95, 10 * 4
)
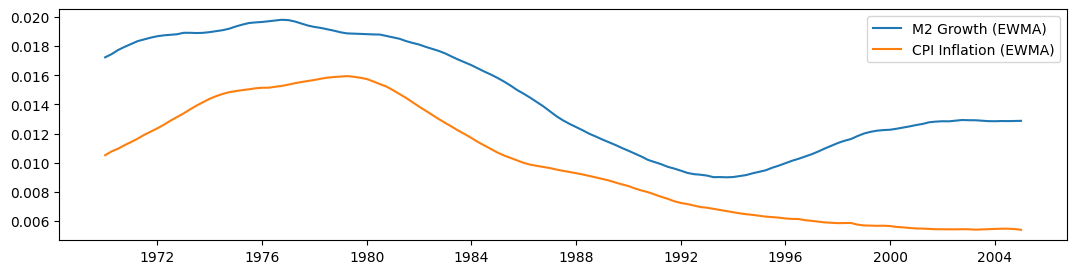
After constructing the moving averages using the \(\beta = 0.95\) filter of Lucas (with a window of 10 years on either side), we plot each of the series below. Although they appear to move together prior for part of the sample, after 1990 they appear to diverge.
[9]:
fig, ax = plt.subplots(figsize=(13, 3))
ax.plot(m2_ewma, label="M2 Growth (EWMA)")
ax.plot(cpi_ewma, label="CPI Inflation (EWMA)")
ax.legend()
[9]:
<matplotlib.legend.Legend at 0x7f36c928ffd0>
[10]:
endog = cpi_ewma
exog = sm.add_constant(m2_ewma)
exog.columns = ["const", "M2"]
mod = sm.RecursiveLS(endog, exog)
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: CPIAUCSL No. Observations: 141
Model: RecursiveLS Log Likelihood 692.878
Date: Thu, 18 Apr 2024 R-squared: 0.813
Time: 09:06:13 AIC -1381.755
Sample: 01-01-1970 BIC -1375.858
- 01-01-2005 HQIC -1379.358
Covariance Type: nonrobust Scale 0.000
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0034 0.001 -6.013 0.000 -0.004 -0.002
M2 0.9128 0.037 24.601 0.000 0.840 0.986
===================================================================================
Ljung-Box (L1) (Q): 138.23 Jarque-Bera (JB): 18.20
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 5.30 Skew: -0.81
Prob(H) (two-sided): 0.00 Kurtosis: 2.27
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
[11]:
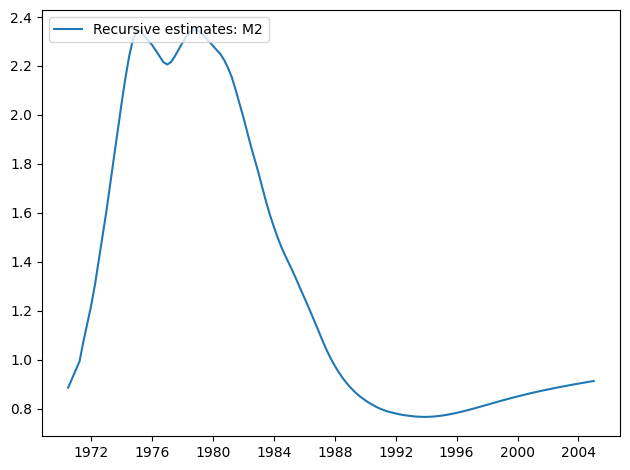
res.plot_recursive_coefficient(1, alpha=None)
[11]:
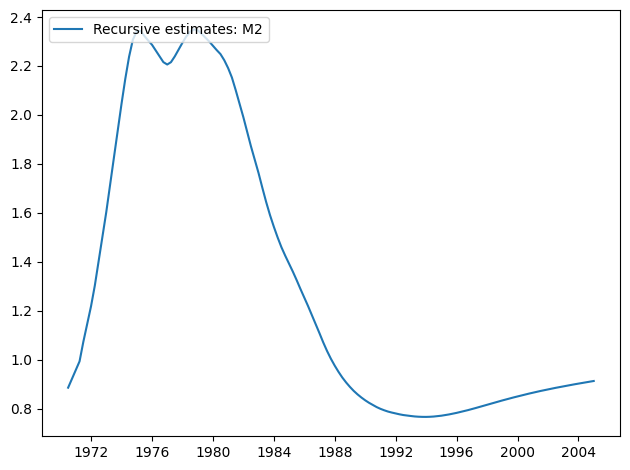
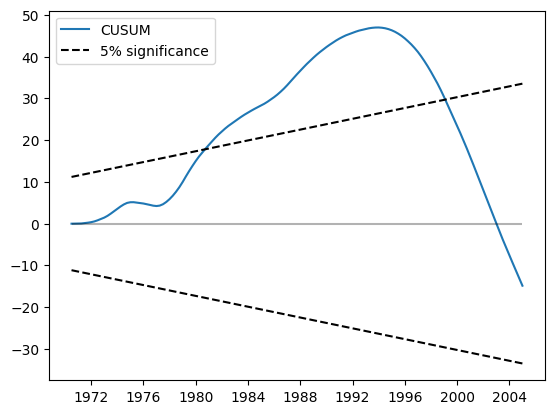
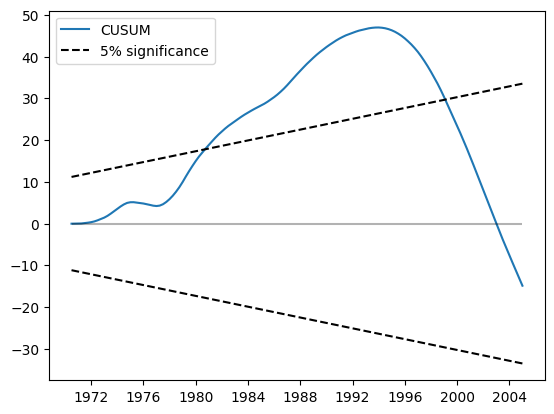
The CUSUM plot now shows substantial deviation at the 5% level, suggesting a rejection of the null hypothesis of parameter stability.
[12]:
res.plot_cusum()
[12]:
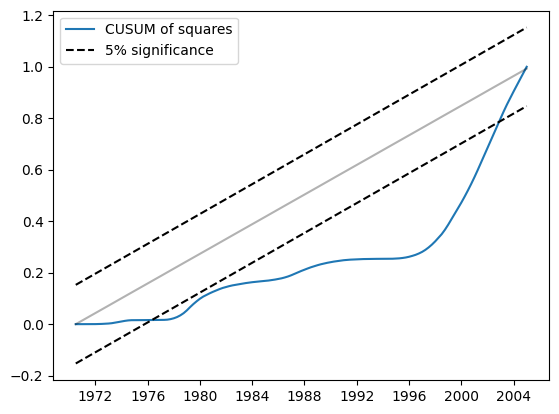
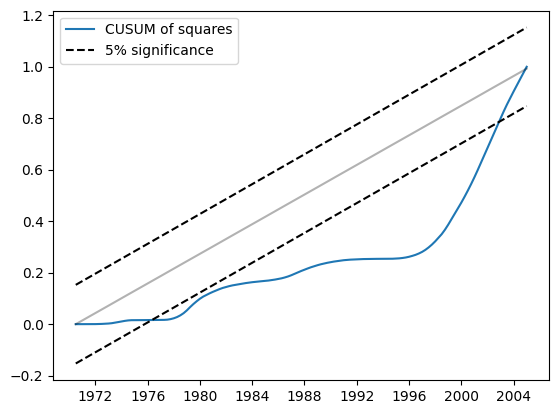
Similarly, the CUSUM of squares shows substantial deviation at the 5% level, also suggesting a rejection of the null hypothesis of parameter stability.
[13]:
res.plot_cusum_squares()
[13]:
Example 3: Linear restrictions and formulas¶
Linear restrictions¶
It is not hard to implement linear restrictions, using the constraints parameter in constructing the model.
[14]:
endog = dta["WORLDCONSUMPTION"]
exog = sm.add_constant(
dta[["COPPERPRICE", "INCOMEINDEX", "ALUMPRICE", "INVENTORYINDEX"]]
)
mod = sm.RecursiveLS(endog, exog, constraints="COPPERPRICE = ALUMPRICE")
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: WORLDCONSUMPTION No. Observations: 25
Model: RecursiveLS Log Likelihood -134.231
Date: Thu, 18 Apr 2024 R-squared: 0.989
Time: 09:06:18 AIC 276.462
Sample: 01-01-1951 BIC 281.338
- 01-01-1975 HQIC 277.814
Covariance Type: nonrobust Scale 137155.014
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
const -4839.4836 2412.410 -2.006 0.045 -9567.721 -111.246
COPPERPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INCOMEINDEX 1.115e+04 666.308 16.738 0.000 9847.000 1.25e+04
ALUMPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INVENTORYINDEX 241.3452 2298.951 0.105 0.916 -4264.515 4747.206
===================================================================================
Ljung-Box (L1) (Q): 6.27 Jarque-Bera (JB): 1.78
Prob(Q): 0.01 Prob(JB): 0.41
Heteroskedasticity (H): 1.75 Skew: -0.63
Prob(H) (two-sided): 0.48 Kurtosis: 2.32
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
Formula¶
One could fit the same model using the class method from_formula.
[15]:
mod = sm.RecursiveLS.from_formula(
"WORLDCONSUMPTION ~ COPPERPRICE + INCOMEINDEX + ALUMPRICE + INVENTORYINDEX",
dta,
constraints="COPPERPRICE = ALUMPRICE",
)
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: WORLDCONSUMPTION No. Observations: 25
Model: RecursiveLS Log Likelihood -134.231
Date: Thu, 18 Apr 2024 R-squared: 0.989
Time: 09:06:18 AIC 276.462
Sample: 01-01-1951 BIC 281.338
- 01-01-1975 HQIC 277.814
Covariance Type: nonrobust Scale 137155.014
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept -4839.4836 2412.410 -2.006 0.045 -9567.721 -111.246
COPPERPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INCOMEINDEX 1.115e+04 666.308 16.738 0.000 9847.000 1.25e+04
ALUMPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INVENTORYINDEX 241.3452 2298.951 0.105 0.916 -4264.515 4747.206
===================================================================================
Ljung-Box (L1) (Q): 6.27 Jarque-Bera (JB): 1.78
Prob(Q): 0.01 Prob(JB): 0.41
Heteroskedasticity (H): 1.75 Skew: -0.63
Prob(H) (two-sided): 0.48 Kurtosis: 2.32
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
/opt/hostedtoolcache/Python/3.10.14/x64/lib/python3.10/site-packages/statsmodels/tsa/base/tsa_model.py:465: ValueWarning: No frequency information was provided, so inferred frequency YS-JAN will be used.
self._init_dates(dates, freq)