Autoregressive Moving Average (ARMA): Artificial data¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
from statsmodels.graphics.tsaplots import plot_predict
from statsmodels.tsa.arima_process import arma_generate_sample
from statsmodels.tsa.arima.model import ARIMA
np.random.seed(12345)
Generate some data from an ARMA process:
[3]:
arparams = np.array([0.75, -0.25])
maparams = np.array([0.65, 0.35])
The conventions of the arma_generate function require that we specify a 1 for the zero-lag of the AR and MA parameters and that the AR parameters be negated.
[4]:
arparams = np.r_[1, -arparams]
maparams = np.r_[1, maparams]
nobs = 250
y = arma_generate_sample(arparams, maparams, nobs)
Now, optionally, we can add some dates information. For this example, we’ll use a pandas time series.
[5]:
dates = pd.date_range("1980-1-1", freq="M", periods=nobs)
y = pd.Series(y, index=dates)
arma_mod = ARIMA(y, order=(2, 0, 2), trend="n")
arma_res = arma_mod.fit()
/tmp/ipykernel_4160/3761908329.py:1: FutureWarning: 'M' is deprecated and will be removed in a future version, please use 'ME' instead.
dates = pd.date_range("1980-1-1", freq="M", periods=nobs)
[6]:
print(arma_res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 250
Model: ARIMA(2, 0, 2) Log Likelihood -353.445
Date: Fri, 19 Apr 2024 AIC 716.891
Time: 16:18:05 BIC 734.498
Sample: 01-31-1980 HQIC 723.977
- 10-31-2000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.7905 0.142 5.566 0.000 0.512 1.069
ar.L2 -0.2314 0.124 -1.859 0.063 -0.475 0.013
ma.L1 0.7007 0.131 5.344 0.000 0.444 0.958
ma.L2 0.4061 0.097 4.177 0.000 0.216 0.597
sigma2 0.9801 0.093 10.514 0.000 0.797 1.163
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 0.29
Prob(Q): 0.96 Prob(JB): 0.86
Heteroskedasticity (H): 0.92 Skew: 0.02
Prob(H) (two-sided): 0.69 Kurtosis: 2.84
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[7]:
y.tail()
[7]:
2000-06-30 0.173211
2000-07-31 -0.048325
2000-08-31 -0.415804
2000-09-30 0.338725
2000-10-31 0.360838
Freq: ME, dtype: float64
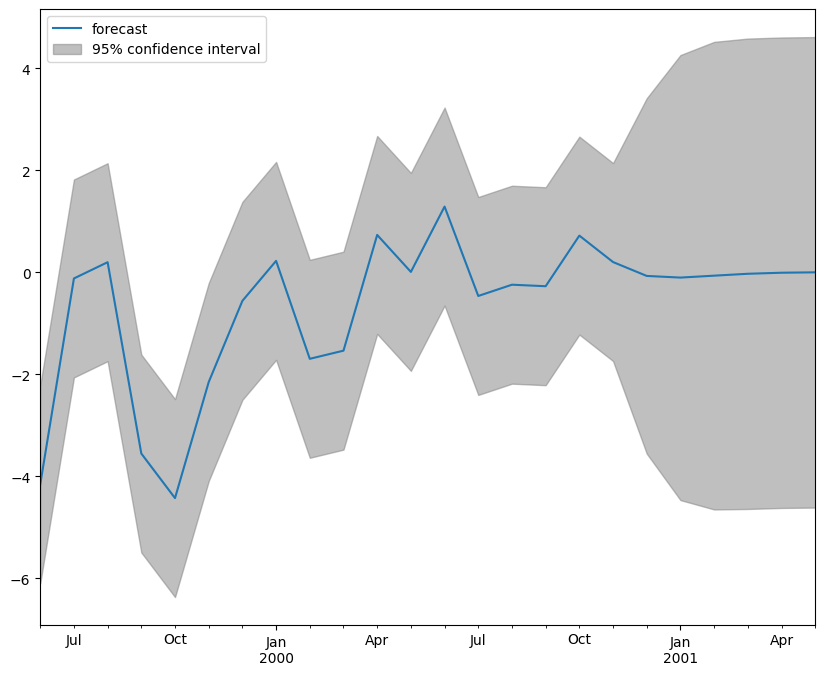
[8]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 8))
fig = plot_predict(arma_res, start="1999-06-30", end="2001-05-31", ax=ax)
legend = ax.legend(loc="upper left")
Last update:
Apr 19, 2024