Prediction (out of sample)¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
Artificial data¶
[3]:
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1 - 5) ** 2))
X = sm.add_constant(X)
beta = [5.0, 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
Estimation¶
[4]:
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.980
Model: OLS Adj. R-squared: 0.979
Method: Least Squares F-statistic: 757.6
Date: Mon, 16 Dec 2024 Prob (F-statistic): 3.79e-39
Time: 11:21:18 Log-Likelihood: -2.3280
No. Observations: 50 AIC: 12.66
Df Residuals: 46 BIC: 20.30
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 5.1848 0.090 57.556 0.000 5.003 5.366
x1 0.4733 0.014 34.066 0.000 0.445 0.501
x2 0.4780 0.055 8.753 0.000 0.368 0.588
x3 -0.0181 0.001 -14.869 0.000 -0.021 -0.016
==============================================================================
Omnibus: 1.503 Durbin-Watson: 2.348
Prob(Omnibus): 0.472 Jarque-Bera (JB): 1.476
Skew: -0.381 Prob(JB): 0.478
Kurtosis: 2.643 Cond. No. 221.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In-sample prediction¶
[5]:
ypred = olsres.predict(X)
print(ypred)
[ 4.73136423 5.18528879 5.60199658 5.95543591 6.228957 6.4180475
6.53107388 6.58790679 6.61665643 6.64905407 6.71523875 6.83880546
7.03292857 7.29819736 7.62251914 7.98310609 8.3502192 8.69205435
8.97996758 9.19318126 9.32219778 9.37035996 9.35330188 9.29638018
9.23050811 9.1870765 9.1927964 9.26531047 9.41029439 9.62052434
9.87706384 10.15237498 10.41484283 10.63396965 10.78538562 10.85485269
10.8406039 10.75363364 10.61589134 10.45667521 10.30781867 10.19846015
10.15025578 10.17382131 10.26698802 10.41515897 10.59370731 10.77202233
10.91853877 11.00592286]
Create a new sample of explanatory variables Xnew, predict and plot¶
[6]:
x1n = np.linspace(20.5, 25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n - 5) ** 2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
[11.00606439 10.88047202 10.6478919 10.35104418 10.04616356 9.78923112
9.62226821 9.56304811 9.60074457 9.69858238]
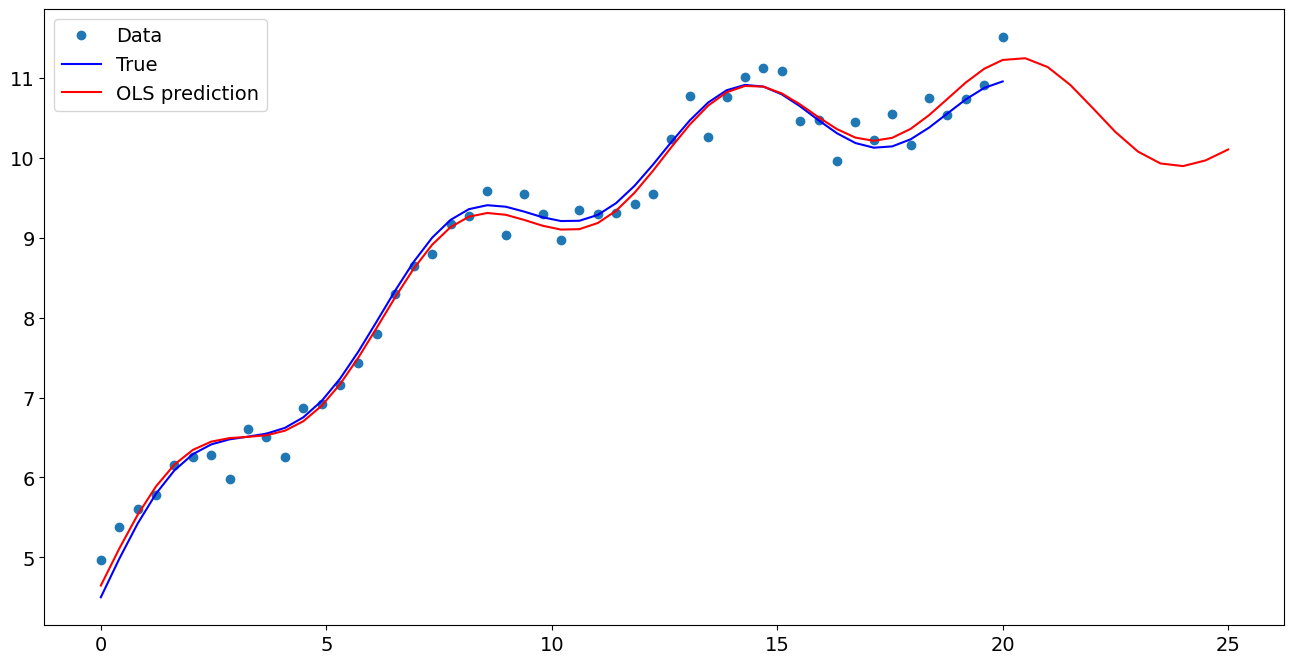
Plot comparison¶
[7]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "r", label="OLS prediction")
ax.legend(loc="best")
[7]:
<matplotlib.legend.Legend at 0x7f6b7ef45150>
Predicting with Formulas¶
Using formulas can make both estimation and prediction a lot easier
[8]:
from statsmodels.formula.api import ols
data = {"x1": x1, "y": y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
We use the I to indicate use of the Identity transform. Ie., we do not want any expansion magic from using **2
[9]:
res.params
[9]:
Intercept 5.184805
x1 0.473284
np.sin(x1) 0.478021
I((x1 - 5) ** 2) -0.018138
dtype: float64
Now we only have to pass the single variable and we get the transformed right-hand side variables automatically
[10]:
res.predict(exog=dict(x1=x1n))
[10]:
0 11.006064
1 10.880472
2 10.647892
3 10.351044
4 10.046164
5 9.789231
6 9.622268
7 9.563048
8 9.600745
9 9.698582
dtype: float64
Last update:
Dec 16, 2024