statsmodels.graphics.gofplots.ProbPlot¶
- class statsmodels.graphics.gofplots.ProbPlot(data, dist=<scipy.stats._continuous_distns.norm_gen object>, fit=False, distargs=(), a=0, loc=0, scale=1)[source]¶
Q-Q and P-P Probability Plots
Can take arguments specifying the parameters for dist or fit them automatically. (See fit under kwargs.)
- Parameters:¶
- data : array_like¶
A 1d data array
- dist : callable
Compare x against dist. A scipy.stats or statsmodels distribution. The default is scipy.stats.distributions.norm (a standard normal). Can be a SciPy frozen distribution.
- fit : bool
If fit is false, loc, scale, and distargs are passed to the distribution. If fit is True then the parameters for dist are fit automatically using dist.fit. The quantiles are formed from the standardized data, after subtracting the fitted loc and dividing by the fitted scale. fit cannot be used if dist is a SciPy frozen distribution.
- distargs : tuple
A tuple of arguments passed to dist to specify it fully so dist.ppf may be called. distargs must not contain loc or scale. These values must be passed using the loc or scale inputs. distargs cannot be used if dist is a SciPy frozen distribution.
- a : float
Offset for the plotting position of an expected order statistic, for example. The plotting positions are given by (i - a)/(nobs - 2*a + 1) for i in range(0,nobs+1)
- loc : float
Location parameter for dist. Cannot be used if dist is a SciPy frozen distribution.
- scale : float
Scale parameter for dist. Cannot be used if dist is a SciPy frozen distribution.
See also
Notes
Depends on matplotlib.
- If fit is True then the parameters are fit using the
distribution’s fit() method.
- The call signatures for the qqplot, ppplot, and probplot
methods are similar, so examples 1 through 4 apply to all three methods.
- The three plotting methods are summarized below:
- ppplotProbability-Probability plot
Compares the sample and theoretical probabilities (percentiles).
- qqplotQuantile-Quantile plot
Compares the sample and theoretical quantiles
- probplotProbability plot
Same as a Q-Q plot, however probabilities are shown in the scale of the theoretical distribution (x-axis) and the y-axis contains unscaled quantiles of the sample data.
Examples
The first example shows a Q-Q plot for regression residuals
>>> # example 1 >>> import statsmodels.api as sm >>> from matplotlib import pyplot as plt >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> model = sm.OLS(data.endog, data.exog) >>> mod_fit = model.fit() >>> res = mod_fit.resid # residuals >>> pplot = sm.ProbPlot(res) >>> fig = pplot.qqplot() >>> h = plt.title("Ex. 1 - qqplot - residuals of OLS fit") >>> plt.show()qqplot of the residuals against quantiles of t-distribution with 4 degrees of freedom:
>>> # example 2 >>> import scipy.stats as stats >>> pplot = sm.ProbPlot(res, stats.t, distargs=(4,)) >>> fig = pplot.qqplot() >>> h = plt.title("Ex. 2 - qqplot - residuals against quantiles of t-dist") >>> plt.show()qqplot against same as above, but with mean 3 and std 10:
>>> # example 3 >>> pplot = sm.ProbPlot(res, stats.t, distargs=(4,), loc=3, scale=10) >>> fig = pplot.qqplot() >>> h = plt.title("Ex. 3 - qqplot - resids vs quantiles of t-dist") >>> plt.show()Automatically determine parameters for t distribution including the loc and scale:
>>> # example 4 >>> pplot = sm.ProbPlot(res, stats.t, fit=True) >>> fig = pplot.qqplot(line="45") >>> h = plt.title("Ex. 4 - qqplot - resids vs. quantiles of fitted t-dist") >>> plt.show()A second ProbPlot object can be used to compare two separate sample sets by using the other kwarg in the qqplot and ppplot methods.
>>> # example 5 >>> import numpy as np >>> x = np.random.normal(loc=8.25, scale=2.75, size=37) >>> y = np.random.normal(loc=8.75, scale=3.25, size=37) >>> pp_x = sm.ProbPlot(x, fit=True) >>> pp_y = sm.ProbPlot(y, fit=True) >>> fig = pp_x.qqplot(line="45", other=pp_y) >>> h = plt.title("Ex. 5 - qqplot - compare two sample sets") >>> plt.show()In qqplot, sample size of other can be equal or larger than the first. In case of larger, size of other samples will be reduced to match the size of the first by interpolation
>>> # example 6 >>> x = np.random.normal(loc=8.25, scale=2.75, size=37) >>> y = np.random.normal(loc=8.75, scale=3.25, size=57) >>> pp_x = sm.ProbPlot(x, fit=True) >>> pp_y = sm.ProbPlot(y, fit=True) >>> fig = pp_x.qqplot(line="45", other=pp_y) >>> title = "Ex. 6 - qqplot - compare different sample sizes" >>> h = plt.title(title) >>> plt.show()In ppplot, sample size of other and the first can be different. other will be used to estimate an empirical cumulative distribution function (ECDF). ECDF(x) will be plotted against p(x)=0.5/n, 1.5/n, …, (n-0.5)/n where x are sorted samples from the first.
>>> # example 7 >>> x = np.random.normal(loc=8.25, scale=2.75, size=37) >>> y = np.random.normal(loc=8.75, scale=3.25, size=57) >>> pp_x = sm.ProbPlot(x, fit=True) >>> pp_y = sm.ProbPlot(y, fit=True) >>> pp_y.ppplot(line="45", other=pp_x) >>> plt.title("Ex. 7A- ppplot - compare two sample sets, other=pp_x") >>> pp_x.ppplot(line="45", other=pp_y) >>> plt.title("Ex. 7B- ppplot - compare two sample sets, other=pp_y") >>> plt.show()The following plot displays some options, follow the link to see the code.
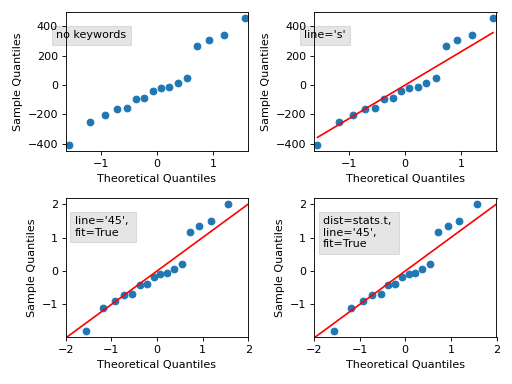
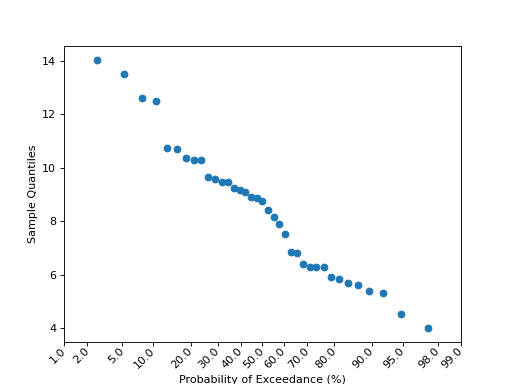
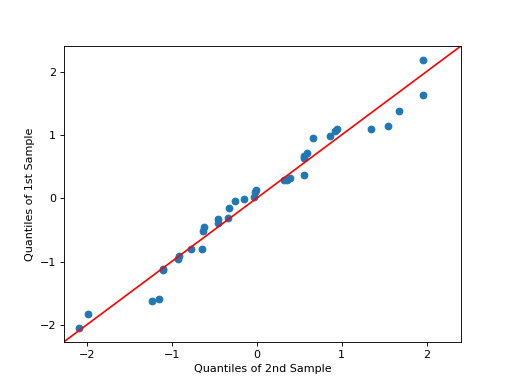
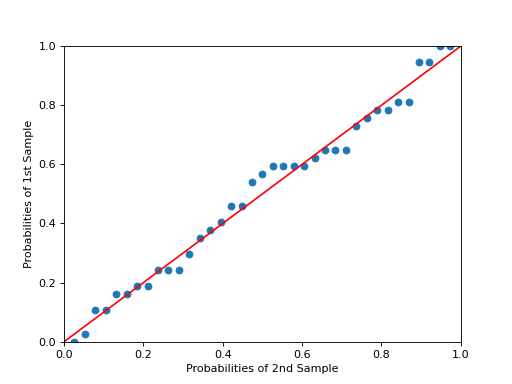
Methods
ppplot([xlabel, ylabel, line, other, ax])Plot of the percentiles of x versus the percentiles of a distribution.
probplot([xlabel, ylabel, line, exceed, ax])Plot of unscaled quantiles of x against the prob of a distribution.
qqplot([xlabel, ylabel, line, other, ax, swap])Plot of the quantiles of x versus the quantiles/ppf of a distribution.
Properties
Sample percentiles
sample quantiles
sorted data
Theoretical percentiles
Theoretical quantiles