Robust Linear Models¶
[1]:
%matplotlib inline
[2]:
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
Estimation¶
Load data:
[3]:
data = sm.datasets.stackloss.load()
data.exog = sm.add_constant(data.exog)
Huber’s T norm with the (default) median absolute deviation scaling
[4]:
huber_t = sm.RLM(data.endog, data.exog, M=sm.robust.norms.HuberT())
hub_results = huber_t.fit()
print(hub_results.params)
print(hub_results.bse)
print(
hub_results.summary(
yname="y", xname=["var_%d" % i for i in range(len(hub_results.params))]
)
)
const -41.026498
AIRFLOW 0.829384
WATERTEMP 0.926066
ACIDCONC -0.127847
dtype: float64
const 9.791899
AIRFLOW 0.111005
WATERTEMP 0.302930
ACIDCONC 0.128650
dtype: float64
Robust linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 21
Model: RLM Df Residuals: 17
Method: IRLS Df Model: 3
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Thu, 12 Mar 2026
Time: 16:08:51
No. Iterations: 19
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
var_0 -41.0265 9.792 -4.190 0.000 -60.218 -21.835
var_1 0.8294 0.111 7.472 0.000 0.612 1.047
var_2 0.9261 0.303 3.057 0.002 0.332 1.520
var_3 -0.1278 0.129 -0.994 0.320 -0.380 0.124
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
Huber’s T norm with ‘H2’ covariance matrix
[5]:
hub_results2 = huber_t.fit(cov="H2")
print(hub_results2.params)
print(hub_results2.bse)
const -41.026498
AIRFLOW 0.829384
WATERTEMP 0.926066
ACIDCONC -0.127847
dtype: float64
const 9.089504
AIRFLOW 0.119460
WATERTEMP 0.322355
ACIDCONC 0.117963
dtype: float64
Andrew’s Wave norm with Huber’s Proposal 2 scaling and ‘H3’ covariance matrix
[6]:
andrew_mod = sm.RLM(data.endog, data.exog, M=sm.robust.norms.AndrewWave())
andrew_results = andrew_mod.fit(scale_est=sm.robust.scale.HuberScale(), cov="H3")
print("Parameters: ", andrew_results.params)
Parameters: const -40.881796
AIRFLOW 0.792761
WATERTEMP 1.048576
ACIDCONC -0.133609
dtype: float64
See help(sm.RLM.fit) for more options and module sm.robust.scale for scale options
Comparing OLS and RLM¶
Artificial data with outliers:
[7]:
nsample = 50
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, (x1 - 5) ** 2))
X = sm.add_constant(X)
sig = 0.3 # smaller error variance makes OLS<->RLM contrast bigger
beta = [5, 0.5, -0.0]
y_true2 = np.dot(X, beta)
y2 = y_true2 + sig * 1.0 * np.random.normal(size=nsample)
y2[[39, 41, 43, 45, 48]] -= 5 # add some outliers (10% of nsample)
Example 1: quadratic function with linear truth¶
Note that the quadratic term in OLS regression will capture outlier effects.
[8]:
res = sm.OLS(y2, X).fit()
print(res.params)
print(res.bse)
print(res.predict())
[ 5.15199914 0.52437172 -0.01551799]
[0.47186918 0.07285023 0.00644612]
[ 4.7640495 5.03883224 5.30844446 5.57288618 5.83215739 6.08625809
6.33518829 6.57894798 6.81753716 7.05095584 7.279204 7.50228166
7.72018881 7.93292546 8.1404916 8.34288723 8.54011235 8.73216696
8.91905107 9.10076467 9.27730776 9.44868035 9.61488243 9.775914
9.93177506 10.08246562 10.22798566 10.36833521 10.50351424 10.63352277
10.75836078 10.8780283 10.9925253 11.1018518 11.20600779 11.30499327
11.39880824 11.48745271 11.57092667 11.64923012 11.72236307 11.7903255
11.85311743 11.91073886 11.96318977 12.01047018 12.05258008 12.08951947
12.12128836 12.14788674]
Estimate RLM:
[9]:
resrlm = sm.RLM(y2, X).fit()
print(resrlm.params)
print(resrlm.bse)
[ 5.07552132e+00 5.10962781e-01 -4.80905625e-03]
[0.15626129 0.02412463 0.00213466]
Draw a plot to compare OLS estimates to the robust estimates:
[10]:
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
ax.plot(x1, y2, "o", label="data")
ax.plot(x1, y_true2, "b-", label="True")
pred_ols = res.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
ax.plot(x1, res.fittedvalues, "r-", label="OLS")
ax.plot(x1, iv_u, "r--")
ax.plot(x1, iv_l, "r--")
ax.plot(x1, resrlm.fittedvalues, "g.-", label="RLM")
ax.legend(loc="best")
[10]:
<matplotlib.legend.Legend at 0x7f003ac84910>
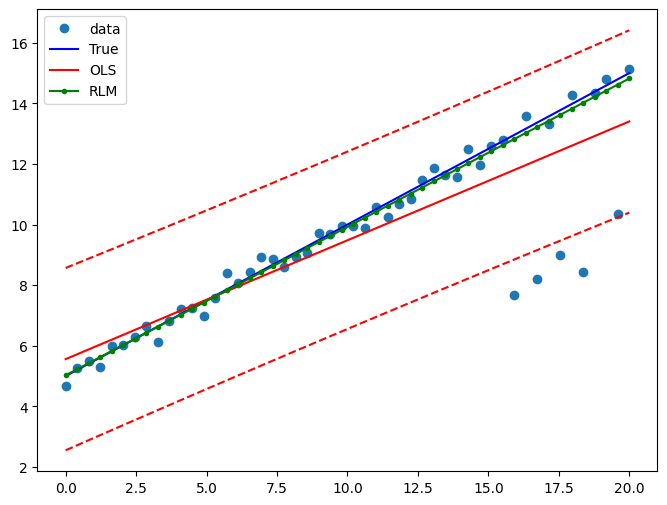
Example 2: linear function with linear truth¶
Fit a new OLS model using only the linear term and the constant:
[11]:
X2 = X[:, [0, 1]]
res2 = sm.OLS(y2, X2).fit()
print(res2.params)
print(res2.bse)
[5.77746895 0.36919186]
[0.41310444 0.03559475]
Estimate RLM:
[12]:
resrlm2 = sm.RLM(y2, X2).fit()
print(resrlm2.params)
print(resrlm2.bse)
[5.22662905 0.46862784]
[0.12651526 0.01090107]
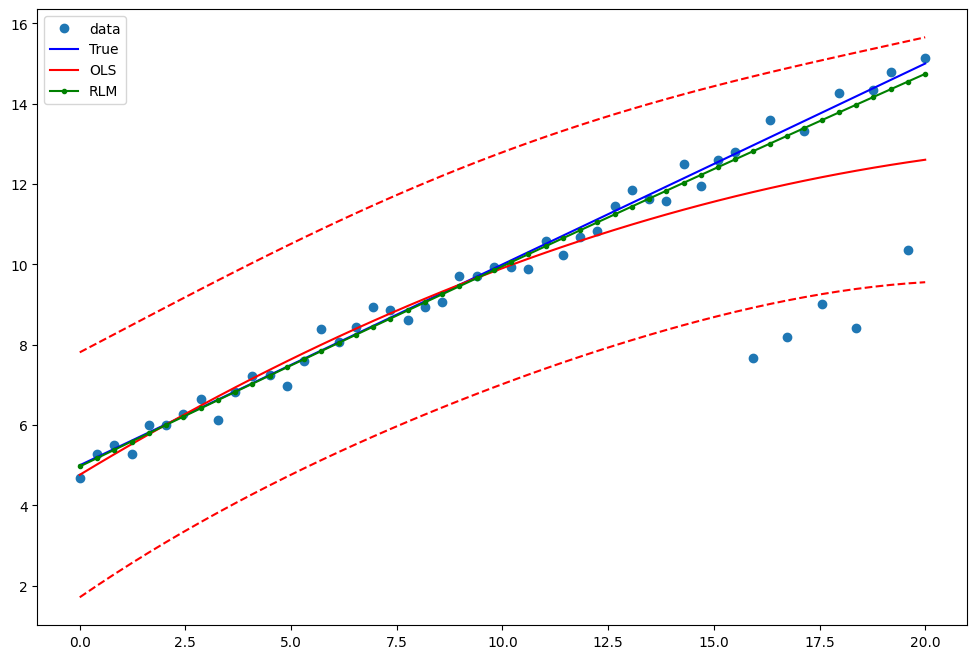
Draw a plot to compare OLS estimates to the robust estimates:
[13]:
pred_ols = res2.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x1, y2, "o", label="data")
ax.plot(x1, y_true2, "b-", label="True")
ax.plot(x1, res2.fittedvalues, "r-", label="OLS")
ax.plot(x1, iv_u, "r--")
ax.plot(x1, iv_l, "r--")
ax.plot(x1, resrlm2.fittedvalues, "g.-", label="RLM")
legend = ax.legend(loc="best")
