Prediction (out of sample)¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rc("figure", figsize=(16,8))
plt.rc("font", size=14)
Artificial data¶
[3]:
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1-5)**2))
X = sm.add_constant(X)
beta = [5., 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
Estimation¶
[4]:
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.989
Model: OLS Adj. R-squared: 0.988
Method: Least Squares F-statistic: 1353.
Date: Tue, 02 Feb 2021 Prob (F-statistic): 7.53e-45
Time: 06:51:34 Log-Likelihood: 9.2333
No. Observations: 50 AIC: -10.47
Df Residuals: 46 BIC: -2.818
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.9077 0.071 68.652 0.000 4.764 5.052
x1 0.5179 0.011 46.976 0.000 0.496 0.540
x2 0.4952 0.043 11.426 0.000 0.408 0.582
x3 -0.0212 0.001 -21.864 0.000 -0.023 -0.019
==============================================================================
Omnibus: 0.349 Durbin-Watson: 2.124
Prob(Omnibus): 0.840 Jarque-Bera (JB): 0.521
Skew: 0.059 Prob(JB): 0.771
Kurtosis: 2.514 Cond. No. 221.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In-sample prediction¶
[5]:
ypred = olsres.predict(X)
print(ypred)
[ 4.37860807 4.86941945 5.3208846 5.70601499 6.00756216 6.22085149
6.35455029 6.42924376 6.47405292 6.52185006 6.60385799 6.74452017
6.95748471 7.24336207 7.58962472 7.97266541 8.36167575 8.72370795
9.02908805 9.25629127 9.39547846 9.45011268 9.43639015 9.38057936
9.31470514 9.27128714 9.2779969 9.3531115 9.50251071 9.71871094
9.98209478 10.26413409 10.53207707 10.75432932 10.90564469 10.97127316
10.94938421 10.85136759 10.69996201 10.52551924 10.36101737 10.23664264
10.17482992 10.1865767 10.26963625 10.40888677 10.57881582 10.74771197
10.88287489 10.95598792]
Create a new sample of explanatory variables Xnew, predict and plot¶
[6]:
x1n = np.linspace(20.5,25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n-5)**2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
[10.93372496 10.78001952 10.51429186 10.18079828 9.83779567 9.54327813
9.34077806 9.24870787 9.25585197 9.32411278]
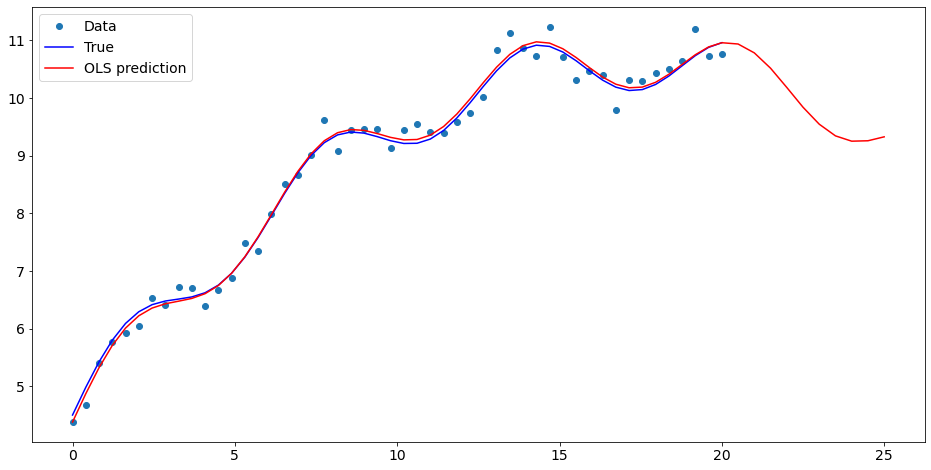
Plot comparison¶
[7]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x1, y, 'o', label="Data")
ax.plot(x1, y_true, 'b-', label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), 'r', label="OLS prediction")
ax.legend(loc="best");
[7]:
<matplotlib.legend.Legend at 0x7fd9b3540150>
Predicting with Formulas¶
Using formulas can make both estimation and prediction a lot easier
[8]:
from statsmodels.formula.api import ols
data = {"x1" : x1, "y" : y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
We use the I to indicate use of the Identity transform. Ie., we do not want any expansion magic from using **2
[9]:
res.params
[9]:
Intercept 4.907719
x1 0.517908
np.sin(x1) 0.495210
I((x1 - 5) ** 2) -0.021164
dtype: float64
Now we only have to pass the single variable and we get the transformed right-hand side variables automatically
[10]:
res.predict(exog=dict(x1=x1n))
[10]:
0 10.933725
1 10.780020
2 10.514292
3 10.180798
4 9.837796
5 9.543278
6 9.340778
7 9.248708
8 9.255852
9 9.324113
dtype: float64