Prediction (out of sample)¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
Artificial data¶
[3]:
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1 - 5) ** 2))
X = sm.add_constant(X)
beta = [5.0, 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
Estimation¶
[4]:
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.986
Model: OLS Adj. R-squared: 0.985
Method: Least Squares F-statistic: 1095.
Date: Fri, 05 May 2023 Prob (F-statistic): 9.24e-43
Time: 13:46:30 Log-Likelihood: 5.5153
No. Observations: 50 AIC: -3.031
Df Residuals: 46 BIC: 4.618
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 5.1190 0.077 66.476 0.000 4.964 5.274
x1 0.4958 0.012 41.750 0.000 0.472 0.520
x2 0.4406 0.047 9.438 0.000 0.347 0.535
x3 -0.0198 0.001 -18.970 0.000 -0.022 -0.018
==============================================================================
Omnibus: 0.463 Durbin-Watson: 2.419
Prob(Omnibus): 0.793 Jarque-Bera (JB): 0.179
Skew: -0.144 Prob(JB): 0.915
Kurtosis: 3.047 Cond. No. 221.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In-sample prediction¶
[5]:
ypred = olsres.predict(X)
print(ypred)
[ 4.62445026 5.0791561 5.49853785 5.85858285 6.14394448 6.35046358
6.48585175 6.56842443 6.62409164 6.68210109 6.77023286 6.91023518
7.1142513 7.38282436 7.70480816 8.05919845 8.41858387 8.75364956
9.03799351 9.25246431 9.38830773 9.44860496 9.44776639 9.40916405
9.36129162 9.33308304 9.34915868 9.42578035 9.5681795 9.76969769
10.0128806 10.27234567 10.51895244 10.7245902 10.86679651 10.93244774
10.91991521 10.8393328 10.71093198 10.56171783 10.42103219 10.31573286
10.26578097 10.28096139 10.35927514 10.48726778 10.64223995 10.79597683
10.91938372 10.98726625]
Create a new sample of explanatory variables Xnew, predict and plot¶
[6]:
x1n = np.linspace(20.5, 25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n - 5) ** 2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
[10.97049523 10.83630035 10.60196055 10.3068523 10.00280887 9.74142978
9.5614474 9.47924392 9.48484044 9.54434013]
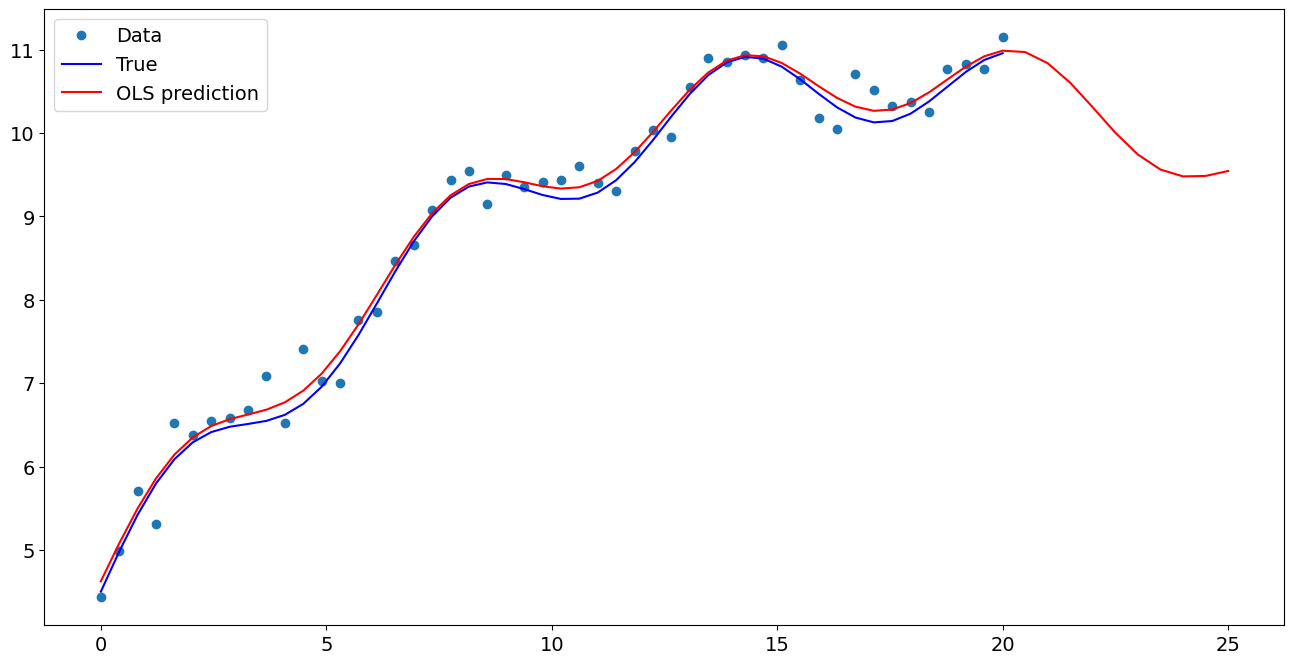
Plot comparison¶
[7]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "r", label="OLS prediction")
ax.legend(loc="best")
[7]:
<matplotlib.legend.Legend at 0x7fceb3698a60>
Predicting with Formulas¶
Using formulas can make both estimation and prediction a lot easier
[8]:
from statsmodels.formula.api import ols
data = {"x1": x1, "y": y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
We use the I to indicate use of the Identity transform. Ie., we do not want any expansion magic from using **2
[9]:
res.params
[9]:
Intercept 5.118951
x1 0.495829
np.sin(x1) 0.440606
I((x1 - 5) ** 2) -0.019780
dtype: float64
Now we only have to pass the single variable and we get the transformed right-hand side variables automatically
[10]:
res.predict(exog=dict(x1=x1n))
[10]:
0 10.970495
1 10.836300
2 10.601961
3 10.306852
4 10.002809
5 9.741430
6 9.561447
7 9.479244
8 9.484840
9 9.544340
dtype: float64
Last update:
May 05, 2023