Prediction (out of sample)¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
Artificial data¶
[3]:
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1 - 5) ** 2))
X = sm.add_constant(X)
beta = [5.0, 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
Estimation¶
[4]:
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.980
Model: OLS Adj. R-squared: 0.979
Method: Least Squares F-statistic: 767.8
Date: Thu, 03 Oct 2024 Prob (F-statistic): 2.80e-39
Time: 15:50:37 Log-Likelihood: -3.6609
No. Observations: 50 AIC: 15.32
Df Residuals: 46 BIC: 22.97
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 5.0304 0.093 54.373 0.000 4.844 5.217
x1 0.5002 0.014 35.058 0.000 0.471 0.529
x2 0.5011 0.056 8.934 0.000 0.388 0.614
x3 -0.0201 0.001 -16.012 0.000 -0.023 -0.018
==============================================================================
Omnibus: 2.155 Durbin-Watson: 1.847
Prob(Omnibus): 0.340 Jarque-Bera (JB): 2.068
Skew: -0.462 Prob(JB): 0.356
Kurtosis: 2.630 Cond. No. 221.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In-sample prediction¶
[5]:
ypred = olsres.predict(X)
print(ypred)
[ 4.52892208 5.01052175 5.45275967 5.82832671 6.11976948 6.32235784
6.44486207 6.50811191 6.54157432 6.57851213 6.65051904 6.7823289
6.98775197 7.26740594 7.60861448 7.98748987 8.37285773 8.73137887
9.03302681 9.25602105 9.39040558 9.43968456 9.42024665 9.35867239
9.28736706 9.23923662 9.24228135 9.31499546 9.46332857 9.67970819
9.94428385 10.2281885 10.49828128 10.72259244 10.87557591 10.94230645
10.9209318 10.82297701 10.67145093 10.49706588 10.33319174 10.21037335
10.15131209 10.1671361 10.25557197 10.40131825 10.57855941 10.75520731
10.89817315 10.97880387]
Create a new sample of explanatory variables Xnew, predict and plot¶
[6]:
x1n = np.linspace(20.5, 25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n - 5) ** 2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
[10.96503747 10.81894524 10.56017815 10.23351824 9.89791447 9.61204991
9.4199741 9.34031818 9.36173334 9.44566941]
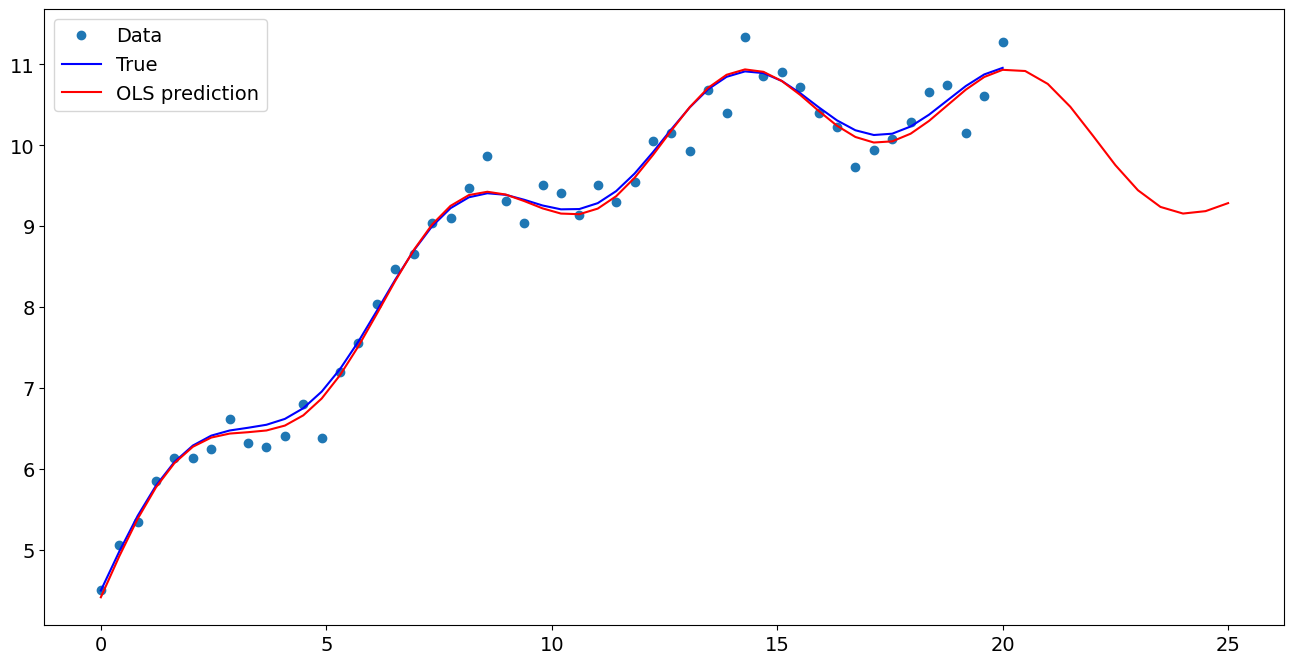
Plot comparison¶
[7]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "r", label="OLS prediction")
ax.legend(loc="best")
[7]:
<matplotlib.legend.Legend at 0x7f30514b3fd0>
Predicting with Formulas¶
Using formulas can make both estimation and prediction a lot easier
[8]:
from statsmodels.formula.api import ols
data = {"x1": x1, "y": y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
We use the I to indicate use of the Identity transform. Ie., we do not want any expansion magic from using **2
[9]:
res.params
[9]:
Intercept 5.030411
x1 0.500216
np.sin(x1) 0.501093
I((x1 - 5) ** 2) -0.020060
dtype: float64
Now we only have to pass the single variable and we get the transformed right-hand side variables automatically
[10]:
res.predict(exog=dict(x1=x1n))
[10]:
0 10.965037
1 10.818945
2 10.560178
3 10.233518
4 9.897914
5 9.612050
6 9.419974
7 9.340318
8 9.361733
9 9.445669
dtype: float64
Last update:
Oct 03, 2024