Linear Regression

Linear models with independently and identically distributed errors, and for errors with heteroscedasticity or autocorrelation. This module allows estimation by ordinary least squares (OLS), weighted least squares (WLS), generalized least squares (GLS), and feasible generalized least squares with autocorrelated AR(p) errors.

See Module Reference for commands and arguments.

Examples

# Load modules and data
import numpy as np
import statsmodels.api as sm
spector_data = sm.datasets.spector.load()
spector_data.exog = sm.add_constant(spector_data.exog, prepend=False)

# Fit and summarize OLS model
mod = sm.OLS(spector_data.endog, spector_data.exog)
res = mod.fit()
print(res.summary())

Detailed examples can be found here:

Technical Documentation

The statistical model is assumed to be

Y = X\beta + \mu, where \mu\sim N\left(0,\sigma^{2}\Sigma\right)

depending on the assumption on 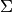\Sigma, we have currently four classes available

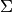
  • GLS : generalized least squares for arbitrary covariance \Sigma
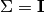
  • OLS : ordinary least squares for i.i.d. errors \Sigma=\textbf{I}
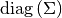
  • WLS : weighted least squares for heteroskedastic errors \text{diag}\left (\Sigma\right)
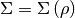
  • GLSAR : feasible generalized least squares with autocorrelated AR(p) errors \Sigma=\Sigma\left(\rho\right)

All regression models define the same methods and follow the same structure, and can be used in a similar fashion. Some of them contain additional model specific methods and attributes.

GLS is the superclass of the other regression classes.

References

General reference for regression models:

  • D.C. Montgomery and E.A. Peck. “Introduction to Linear Regression Analysis.” 2nd. Ed., Wiley, 1992.

Econometrics references for regression models:

  • R.Davidson and J.G. MacKinnon. “Econometric Theory and Methods,” Oxford, 2004.
  • W.Green. “Econometric Analysis,” 5th ed., Pearson, 2003.

Attributes

The following is more verbose description of the attributes which is mostly common to all regression classes

pinv_wexog : array
pinv_wexog is the p x n Moore-Penrose pseudoinverse of the
whitened design matrix. Approximately equal to
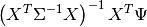\left(X^{T}\Sigma^{-1}X\right)^{-1}X^{T}\Psi
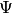where \Psi is given by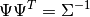 \Psi\Psi^{T}=\Sigma^{-1}
cholsimgainv : array
n x n upper triangular matrix such that
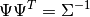
\Psi\Psi^{T}=\Sigma^{-1}
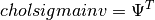
cholsigmainv=\Psi^{T}
df_model : float
The model degrees of freedom is equal to p - 1, where p is the number of regressors. Note that the intercept is not counted as using a degree of freedom here.
df_resid : float
The residual degrees of freedom is equal to the number of observations n less the number of parameters p. Note that the intercept is counted as using a degree of freedom here.
llf : float
The value of the likelihood function of the fitted model.
nobs : float
The number of observations n
normalized_cov_params : array
A p x p array
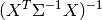
(X^{T}\Sigma^{-1}X)^{-1}
sigma : array
sigma is the n x n strucutre of the covariance matrix of the error terms
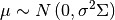
\mu\sim N\left(0,\sigma^{2}\Sigma\right)
wexog : array
wexog is the whitened design matrix.
\Psi^{T}X
wendog : array
The whitened response variable.
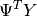
\Psi^{T}Y

Module Reference

Model Classes

OLS(endog[, exog, missing, hasconst]) A simple ordinary least squares model.
GLS(endog, exog[, sigma, missing, hasconst]) Generalized least squares model with a general covariance structure.
WLS(endog, exog[, weights, missing, hasconst]) A regression model with diagonal but non-identity covariance structure.
GLSAR(endog[, exog, rho, missing]) A regression model with an AR(p) covariance structure.
yule_walker(X[, order, method, df, inv, demean]) Estimate AR(p) parameters from a sequence X using Yule-Walker equation.
QuantReg(endog, exog, **kwargs) Quantile Regression

Results Classes

Fitting a linear regression model returns a results class. OLS has a specific results class with some additional methods compared to the results class of the other linear models.

RegressionResults(model, params[, ...]) This class summarizes the fit of a linear regression model.
OLSResults(model, params[, ...]) Results class for for an OLS model.
QuantRegResults(model, params[, ...]) Results instance for the QuantReg model