Autoregressions¶
This notebook introduces autoregression modeling using the AutoReg model. It also covers aspects of ar_select_order assists in selecting models that minimize an information criteria such as the AIC. An autoregressive model has dynamics given by
AutoReg also permits models with:
Deterministic terms (
trend)n: No deterministic termc: Constant (default)ct: Constant and time trendt: Time trend only
Seasonal dummies (
seasonal)Trueincludes \(s-1\) dummies where \(s\) is the period of the time series (e.g., 12 for monthly)
Custom deterministic terms (
deterministic)Accepts a
DeterministicProcess
Exogenous variables (
exog)A
DataFrameorarrayof exogenous variables to include in the model
Omission of selected lags (
lags)If
lagsis an iterable of integers, then only these are included in the model.
The complete specification is
where:
\(d_i\) is a seasonal dummy that is 1 if \(mod(t, period) = i\). Period 0 is excluded if the model contains a constant (
cis intrend).\(t\) is a time trend (\(1,2,\ldots\)) that starts with 1 in the first observation.
\(x_{t,j}\) are exogenous regressors. Note these are time-aligned to the left-hand-side variable when defining a model.
\(\epsilon_t\) is assumed to be a white noise process.
This first cell imports standard packages and sets plots to appear inline.
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
from statsmodels.tsa.api import acf, graphics, pacf
from statsmodels.tsa.ar_model import AutoReg, ar_select_order
This cell sets the plotting style, registers pandas date converters for matplotlib, and sets the default figure size.
[2]:
sns.set_style("darkgrid")
pd.plotting.register_matplotlib_converters()
# Default figure size
sns.mpl.rc("figure", figsize=(16, 6))
sns.mpl.rc("font", size=14)
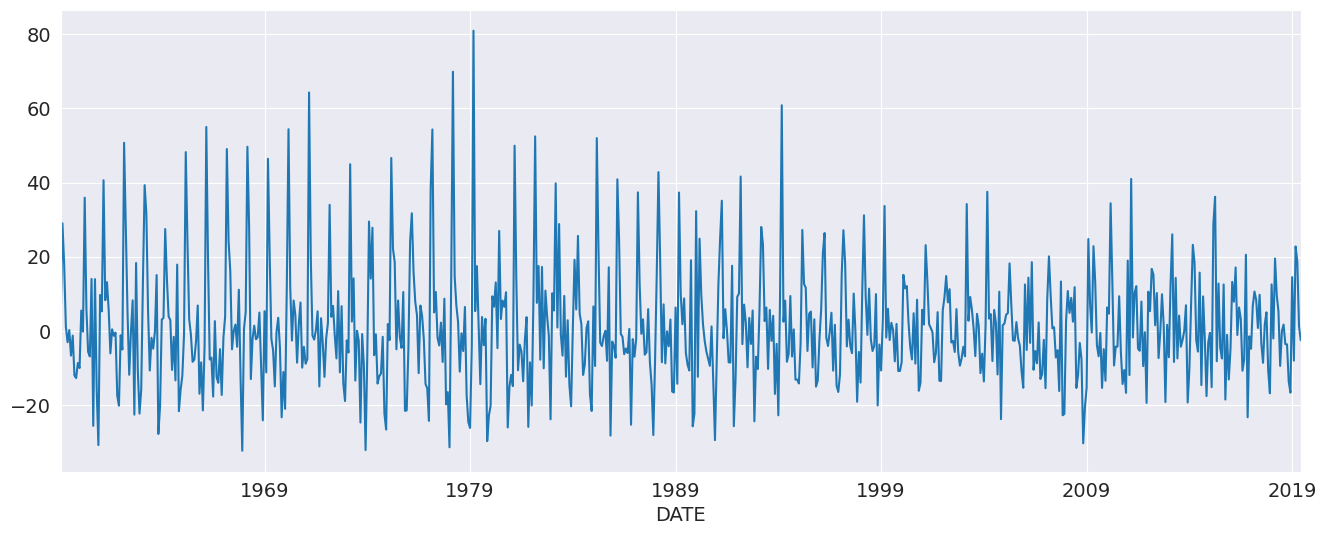
The first set of examples uses the month-over-month growth rate in U.S. Housing starts that has not been seasonally adjusted. The seasonality is evident by the regular pattern of peaks and troughs. We set the frequency for the time series to “MS” (month-start) to avoid warnings when using AutoReg.
[3]:
data = pdr.get_data_fred("HOUSTNSA", "1959-01-01", "2019-06-01")
housing = data.HOUSTNSA.pct_change().dropna()
# Scale by 100 to get percentages
housing = 100 * housing.asfreq("MS")
fig, ax = plt.subplots()
ax = housing.plot(ax=ax)
We can start with an AR(3). While this is not a good model for this data, it demonstrates the basic use of the API.
[4]:
mod = AutoReg(housing, 3, old_names=False)
res = mod.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(3) Log Likelihood -2993.442
Method: Conditional MLE S.D. of innovations 15.289
Date: Thu, 03 Oct 2024 AIC 5996.884
Time: 15:55:21 BIC 6019.794
Sample: 05-01-1959 HQIC 6005.727
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.1228 0.573 1.961 0.050 0.000 2.245
HOUSTNSA.L1 0.1910 0.036 5.235 0.000 0.120 0.263
HOUSTNSA.L2 0.0058 0.037 0.155 0.877 -0.067 0.079
HOUSTNSA.L3 -0.1939 0.036 -5.319 0.000 -0.265 -0.122
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9680 -1.3298j 1.6448 -0.1499
AR.2 0.9680 +1.3298j 1.6448 0.1499
AR.3 -1.9064 -0.0000j 1.9064 -0.5000
-----------------------------------------------------------------------------
AutoReg supports the same covariance estimators as OLS. Below, we use cov_type="HC0", which is White’s covariance estimator. While the parameter estimates are the same, all of the quantities that depend on the standard error change.
[5]:
res = mod.fit(cov_type="HC0")
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(3) Log Likelihood -2993.442
Method: Conditional MLE S.D. of innovations 15.289
Date: Thu, 03 Oct 2024 AIC 5996.884
Time: 15:55:21 BIC 6019.794
Sample: 05-01-1959 HQIC 6005.727
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.1228 0.601 1.869 0.062 -0.055 2.300
HOUSTNSA.L1 0.1910 0.035 5.499 0.000 0.123 0.259
HOUSTNSA.L2 0.0058 0.039 0.150 0.881 -0.070 0.081
HOUSTNSA.L3 -0.1939 0.036 -5.448 0.000 -0.264 -0.124
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9680 -1.3298j 1.6448 -0.1499
AR.2 0.9680 +1.3298j 1.6448 0.1499
AR.3 -1.9064 -0.0000j 1.9064 -0.5000
-----------------------------------------------------------------------------
[6]:
sel = ar_select_order(housing, 13, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(13) Log Likelihood -2676.157
Method: Conditional MLE S.D. of innovations 10.378
Date: Thu, 03 Oct 2024 AIC 5382.314
Time: 15:55:21 BIC 5450.835
Sample: 03-01-1960 HQIC 5408.781
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 1.3615 0.458 2.970 0.003 0.463 2.260
HOUSTNSA.L1 -0.2900 0.036 -8.161 0.000 -0.360 -0.220
HOUSTNSA.L2 -0.0828 0.031 -2.652 0.008 -0.144 -0.022
HOUSTNSA.L3 -0.0654 0.031 -2.106 0.035 -0.126 -0.005
HOUSTNSA.L4 -0.1596 0.031 -5.166 0.000 -0.220 -0.099
HOUSTNSA.L5 -0.0434 0.031 -1.387 0.165 -0.105 0.018
HOUSTNSA.L6 -0.0884 0.031 -2.867 0.004 -0.149 -0.028
HOUSTNSA.L7 -0.0556 0.031 -1.797 0.072 -0.116 0.005
HOUSTNSA.L8 -0.1482 0.031 -4.803 0.000 -0.209 -0.088
HOUSTNSA.L9 -0.0926 0.031 -2.960 0.003 -0.154 -0.031
HOUSTNSA.L10 -0.1133 0.031 -3.665 0.000 -0.174 -0.053
HOUSTNSA.L11 0.1151 0.031 3.699 0.000 0.054 0.176
HOUSTNSA.L12 0.5352 0.031 17.133 0.000 0.474 0.596
HOUSTNSA.L13 0.3178 0.036 8.937 0.000 0.248 0.388
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 1.0913 -0.0000j 1.0913 -0.0000
AR.2 0.8743 -0.5018j 1.0080 -0.0829
AR.3 0.8743 +0.5018j 1.0080 0.0829
AR.4 0.5041 -0.8765j 1.0111 -0.1669
AR.5 0.5041 +0.8765j 1.0111 0.1669
AR.6 0.0056 -1.0530j 1.0530 -0.2491
AR.7 0.0056 +1.0530j 1.0530 0.2491
AR.8 -0.5263 -0.9335j 1.0716 -0.3317
AR.9 -0.5263 +0.9335j 1.0716 0.3317
AR.10 -0.9525 -0.5880j 1.1194 -0.4120
AR.11 -0.9525 +0.5880j 1.1194 0.4120
AR.12 -1.2928 -0.2608j 1.3189 -0.4683
AR.13 -1.2928 +0.2608j 1.3189 0.4683
------------------------------------------------------------------------------
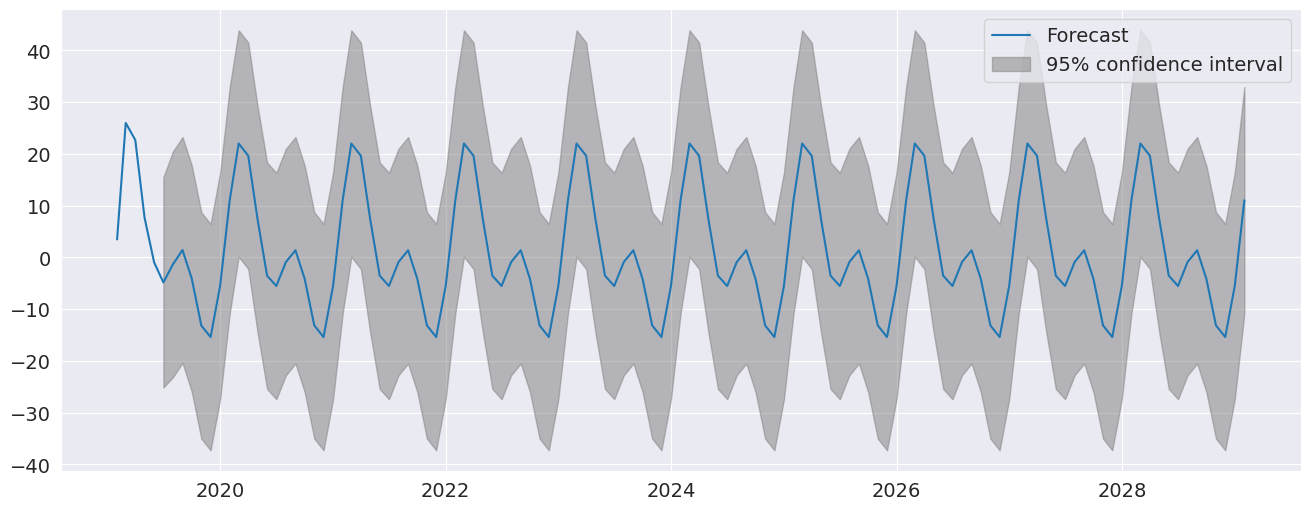
plot_predict visualizes forecasts. Here we produce a large number of forecasts which show the string seasonality captured by the model.
[7]:
fig = res.plot_predict(720, 840)
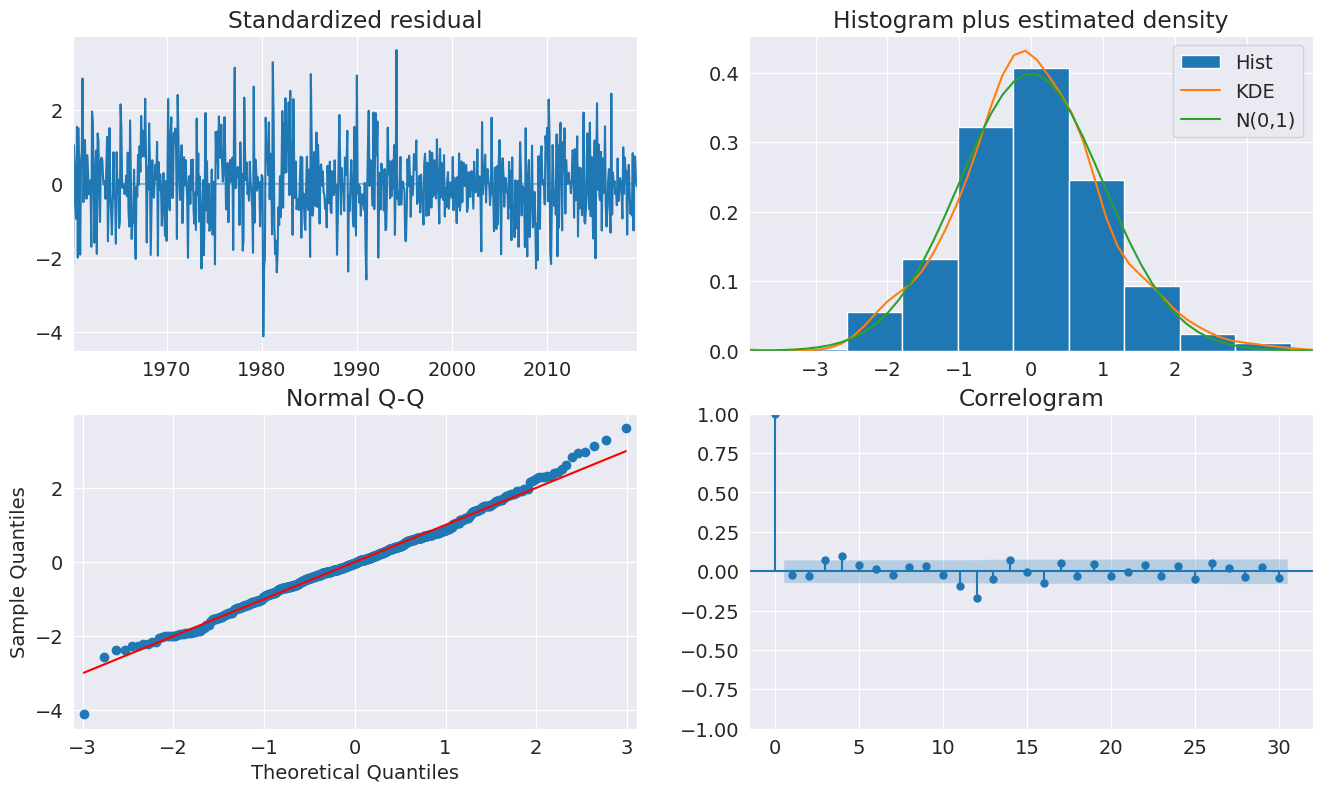
plot_diagnositcs indicates that the model captures the key features in the data.
[8]:
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)
Seasonal Dummies¶
AutoReg supports seasonal dummies which are an alternative way to model seasonality. Including the dummies shortens the dynamics to only an AR(2).
[9]:
sel = ar_select_order(housing, 13, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: Seas. AutoReg(2) Log Likelihood -2652.556
Method: Conditional MLE S.D. of innovations 9.487
Date: Thu, 03 Oct 2024 AIC 5335.112
Time: 15:55:27 BIC 5403.863
Sample: 04-01-1959 HQIC 5361.648
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.2726 1.373 0.927 0.354 -1.418 3.963
s(2,12) 32.6477 1.824 17.901 0.000 29.073 36.222
s(3,12) 23.0685 2.435 9.472 0.000 18.295 27.842
s(4,12) 10.7267 2.693 3.983 0.000 5.449 16.005
s(5,12) 1.6792 2.100 0.799 0.424 -2.437 5.796
s(6,12) -4.4229 1.896 -2.333 0.020 -8.138 -0.707
s(7,12) -4.2113 1.824 -2.309 0.021 -7.786 -0.636
s(8,12) -6.4124 1.791 -3.581 0.000 -9.922 -2.902
s(9,12) 0.1095 1.800 0.061 0.952 -3.419 3.638
s(10,12) -16.7511 1.814 -9.234 0.000 -20.307 -13.196
s(11,12) -20.7023 1.862 -11.117 0.000 -24.352 -17.053
s(12,12) -11.9554 1.778 -6.724 0.000 -15.440 -8.470
HOUSTNSA.L1 -0.2953 0.037 -7.994 0.000 -0.368 -0.223
HOUSTNSA.L2 -0.1148 0.037 -3.107 0.002 -0.187 -0.042
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.2862 -2.6564j 2.9514 -0.3218
AR.2 -1.2862 +2.6564j 2.9514 0.3218
-----------------------------------------------------------------------------
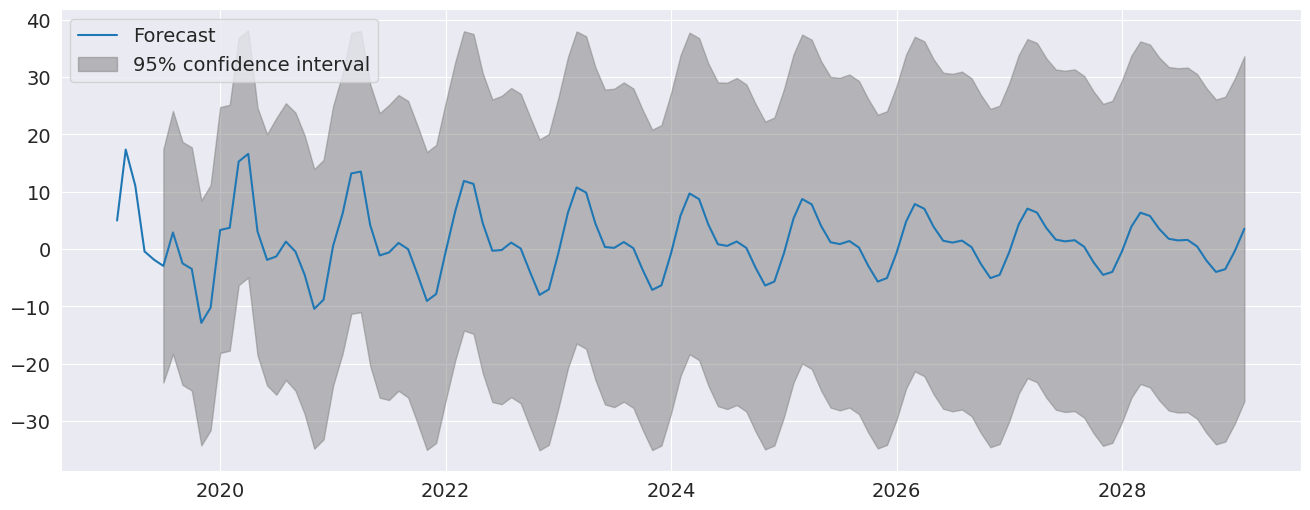
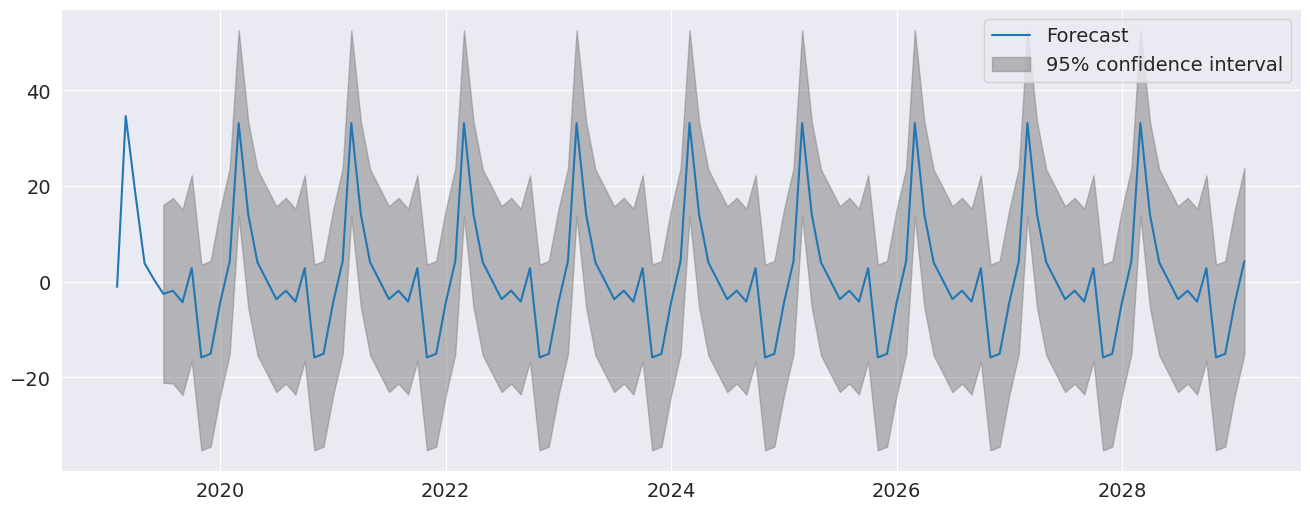
The seasonal dummies are obvious in the forecasts which has a non-trivial seasonal component in all periods 10 years in to the future.
[10]:
fig = res.plot_predict(720, 840)
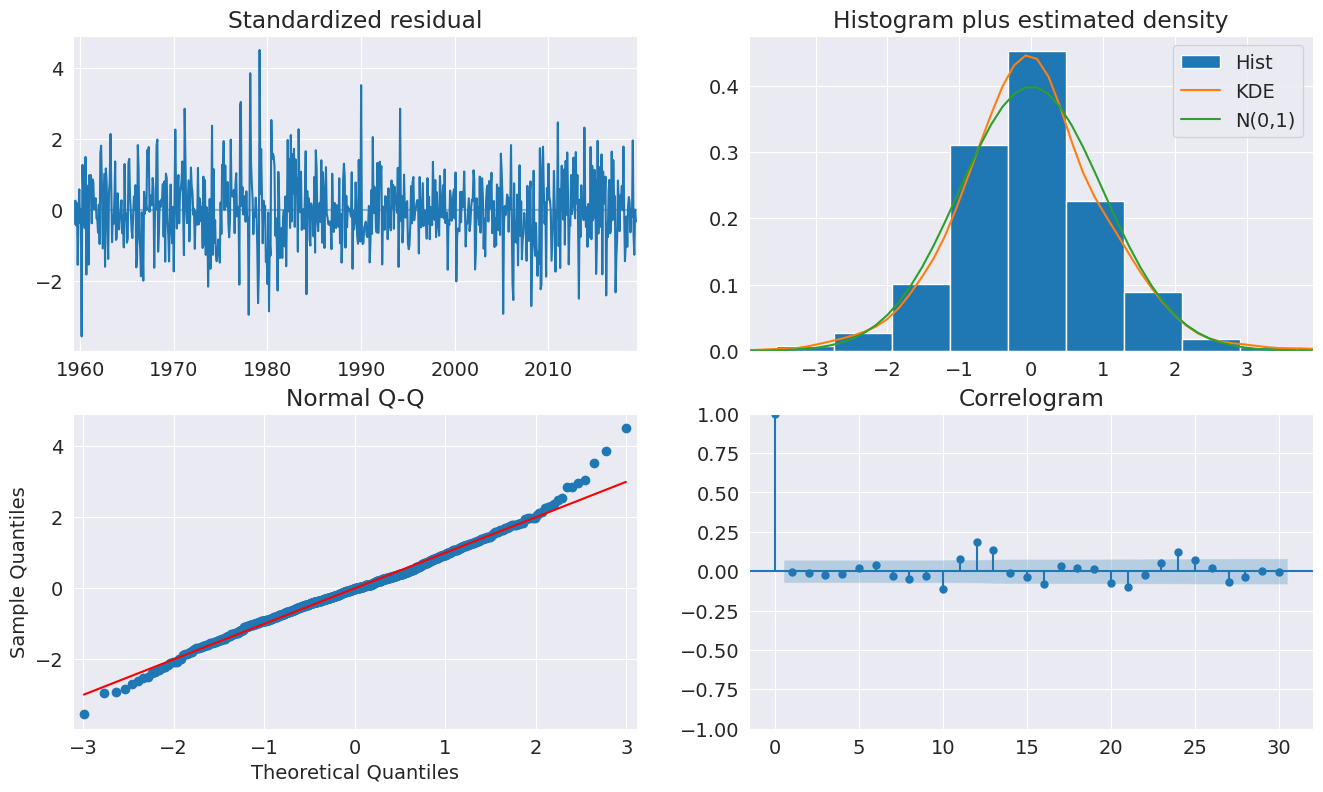
[11]:
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(lags=30, fig=fig)
Seasonal Dynamics¶
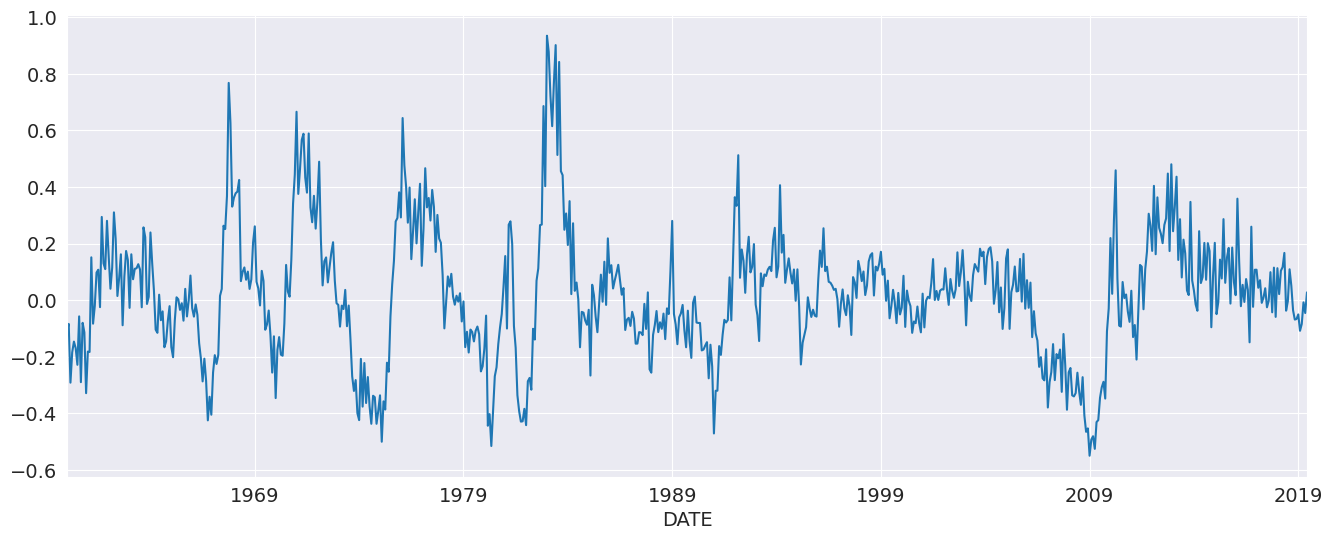
While AutoReg does not directly support Seasonal components since it uses OLS to estimate parameters, it is possible to capture seasonal dynamics using an over-parametrized Seasonal AR that does not impose the restrictions in the Seasonal AR.
[12]:
yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()
_, ax = plt.subplots()
ax = yoy_housing.plot(ax=ax)
We start by selecting a model using the simple method that only chooses the maximum lag. All lower lags are automatically included. The maximum lag to check is set to 13 since this allows the model to next a Seasonal AR that has both a short-run AR(1) component and a Seasonal AR(1) component, so that
which becomes
when expanded. AutoReg does not enforce the structure, but can estimate the nesting model
We see that all 13 lags are selected.
[13]:
sel = ar_select_order(yoy_housing, 13, old_names=False)
sel.ar_lags
[13]:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
It seems unlikely that all 13 lags are required. We can set glob=True to search all \(2^{13}\) models that include up to 13 lags.
Here we see that the first three are selected, as is the 7th, and finally the 12th and 13th are selected. This is superficially similar to the structure described above.
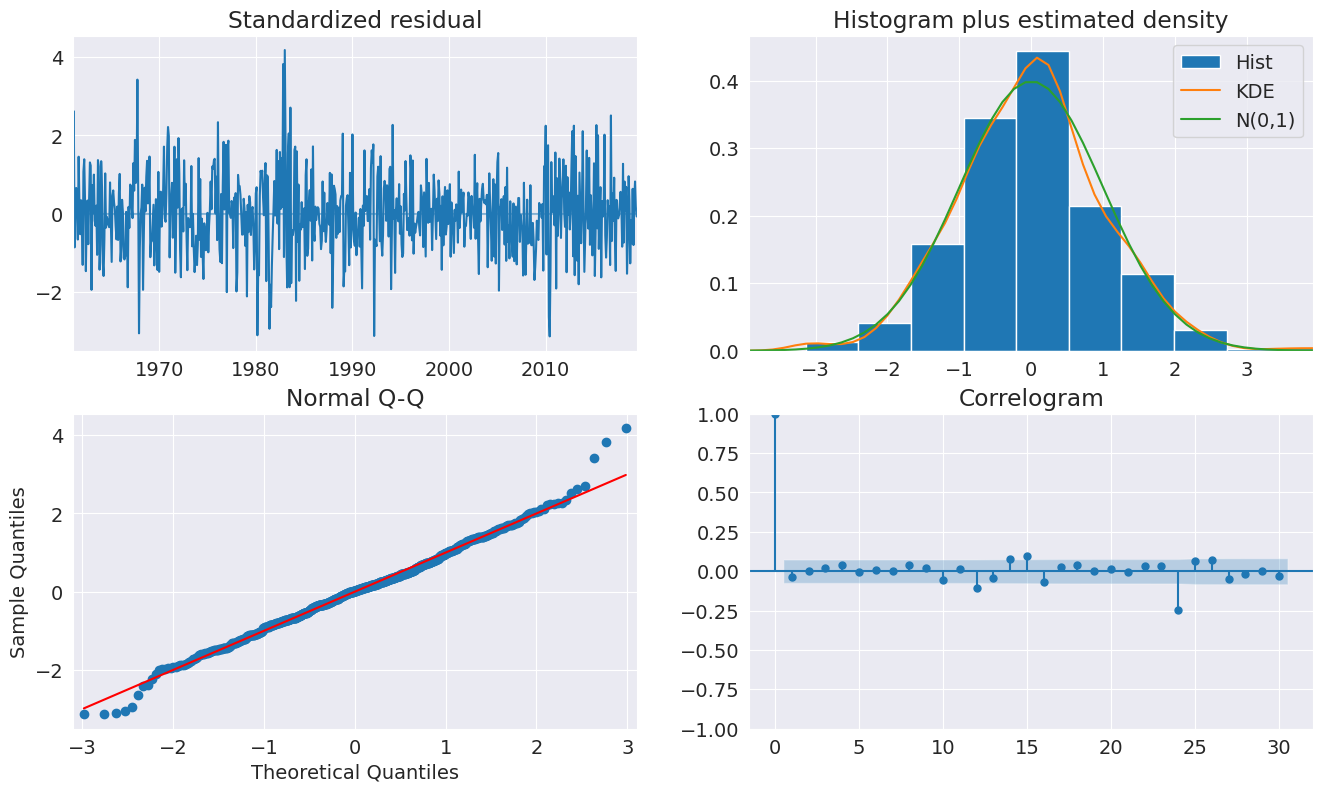
After fitting the model, we take a look at the diagnostic plots that indicate that this specification appears to be adequate to capture the dynamics in the data.
[14]:
sel = ar_select_order(yoy_housing, 13, glob=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 714
Model: Restr. AutoReg(13) Log Likelihood 589.177
Method: Conditional MLE S.D. of innovations 0.104
Date: Thu, 03 Oct 2024 AIC -1162.353
Time: 15:55:45 BIC -1125.933
Sample: 02-01-1961 HQIC -1148.276
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 0.0035 0.004 0.875 0.382 -0.004 0.011
HOUSTNSA.L1 0.5640 0.035 16.167 0.000 0.496 0.632
HOUSTNSA.L2 0.2347 0.038 6.238 0.000 0.161 0.308
HOUSTNSA.L3 0.2051 0.037 5.560 0.000 0.133 0.277
HOUSTNSA.L7 -0.0903 0.030 -2.976 0.003 -0.150 -0.031
HOUSTNSA.L12 -0.3791 0.034 -11.075 0.000 -0.446 -0.312
HOUSTNSA.L13 0.3354 0.033 10.254 0.000 0.271 0.400
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0309 -0.2682j 1.0652 -0.4595
AR.2 -1.0309 +0.2682j 1.0652 0.4595
AR.3 -0.7454 -0.7417j 1.0515 -0.3754
AR.4 -0.7454 +0.7417j 1.0515 0.3754
AR.5 -0.3172 -1.0221j 1.0702 -0.2979
AR.6 -0.3172 +1.0221j 1.0702 0.2979
AR.7 0.2419 -1.0573j 1.0846 -0.2142
AR.8 0.2419 +1.0573j 1.0846 0.2142
AR.9 0.7840 -0.8303j 1.1420 -0.1296
AR.10 0.7840 +0.8303j 1.1420 0.1296
AR.11 1.0730 -0.2386j 1.0992 -0.0348
AR.12 1.0730 +0.2386j 1.0992 0.0348
AR.13 1.1193 -0.0000j 1.1193 -0.0000
------------------------------------------------------------------------------
[15]:
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)
We can also include seasonal dummies. These are all insignificant since the model is using year-over-year changes.
[16]:
sel = ar_select_order(yoy_housing, 13, glob=True, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
====================================================================================
Dep. Variable: HOUSTNSA No. Observations: 714
Model: Restr. Seas. AutoReg(13) Log Likelihood 590.875
Method: Conditional MLE S.D. of innovations 0.104
Date: Thu, 03 Oct 2024 AIC -1143.751
Time: 16:08:11 BIC -1057.253
Sample: 02-01-1961 HQIC -1110.317
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 0.0167 0.014 1.215 0.224 -0.010 0.044
s(2,12) -0.0179 0.019 -0.931 0.352 -0.056 0.020
s(3,12) -0.0121 0.019 -0.630 0.528 -0.050 0.026
s(4,12) -0.0210 0.019 -1.089 0.276 -0.059 0.017
s(5,12) -0.0223 0.019 -1.157 0.247 -0.060 0.015
s(6,12) -0.0224 0.019 -1.160 0.246 -0.060 0.015
s(7,12) -0.0212 0.019 -1.096 0.273 -0.059 0.017
s(8,12) -0.0101 0.019 -0.520 0.603 -0.048 0.028
s(9,12) -0.0095 0.019 -0.491 0.623 -0.047 0.028
s(10,12) -0.0049 0.019 -0.252 0.801 -0.043 0.033
s(11,12) -0.0084 0.019 -0.435 0.664 -0.046 0.030
s(12,12) -0.0077 0.019 -0.400 0.689 -0.046 0.030
HOUSTNSA.L1 0.5630 0.035 16.160 0.000 0.495 0.631
HOUSTNSA.L2 0.2347 0.038 6.248 0.000 0.161 0.308
HOUSTNSA.L3 0.2075 0.037 5.634 0.000 0.135 0.280
HOUSTNSA.L7 -0.0916 0.030 -3.013 0.003 -0.151 -0.032
HOUSTNSA.L12 -0.3810 0.034 -11.149 0.000 -0.448 -0.314
HOUSTNSA.L13 0.3373 0.033 10.327 0.000 0.273 0.401
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0305 -0.2681j 1.0648 -0.4595
AR.2 -1.0305 +0.2681j 1.0648 0.4595
AR.3 -0.7447 -0.7414j 1.0509 -0.3754
AR.4 -0.7447 +0.7414j 1.0509 0.3754
AR.5 -0.3172 -1.0215j 1.0696 -0.2979
AR.6 -0.3172 +1.0215j 1.0696 0.2979
AR.7 0.2416 -1.0568j 1.0841 -0.2142
AR.8 0.2416 +1.0568j 1.0841 0.2142
AR.9 0.7837 -0.8304j 1.1418 -0.1296
AR.10 0.7837 +0.8304j 1.1418 0.1296
AR.11 1.0724 -0.2383j 1.0986 -0.0348
AR.12 1.0724 +0.2383j 1.0986 0.0348
AR.13 1.1192 -0.0000j 1.1192 -0.0000
------------------------------------------------------------------------------
Industrial Production¶
We will use the industrial production index data to examine forecasting.
[17]:
data = pdr.get_data_fred("INDPRO", "1959-01-01", "2019-06-01")
ind_prod = data.INDPRO.pct_change(12).dropna().asfreq("MS")
_, ax = plt.subplots(figsize=(16, 9))
ind_prod.plot(ax=ax)
[17]:
<Axes: xlabel='DATE'>
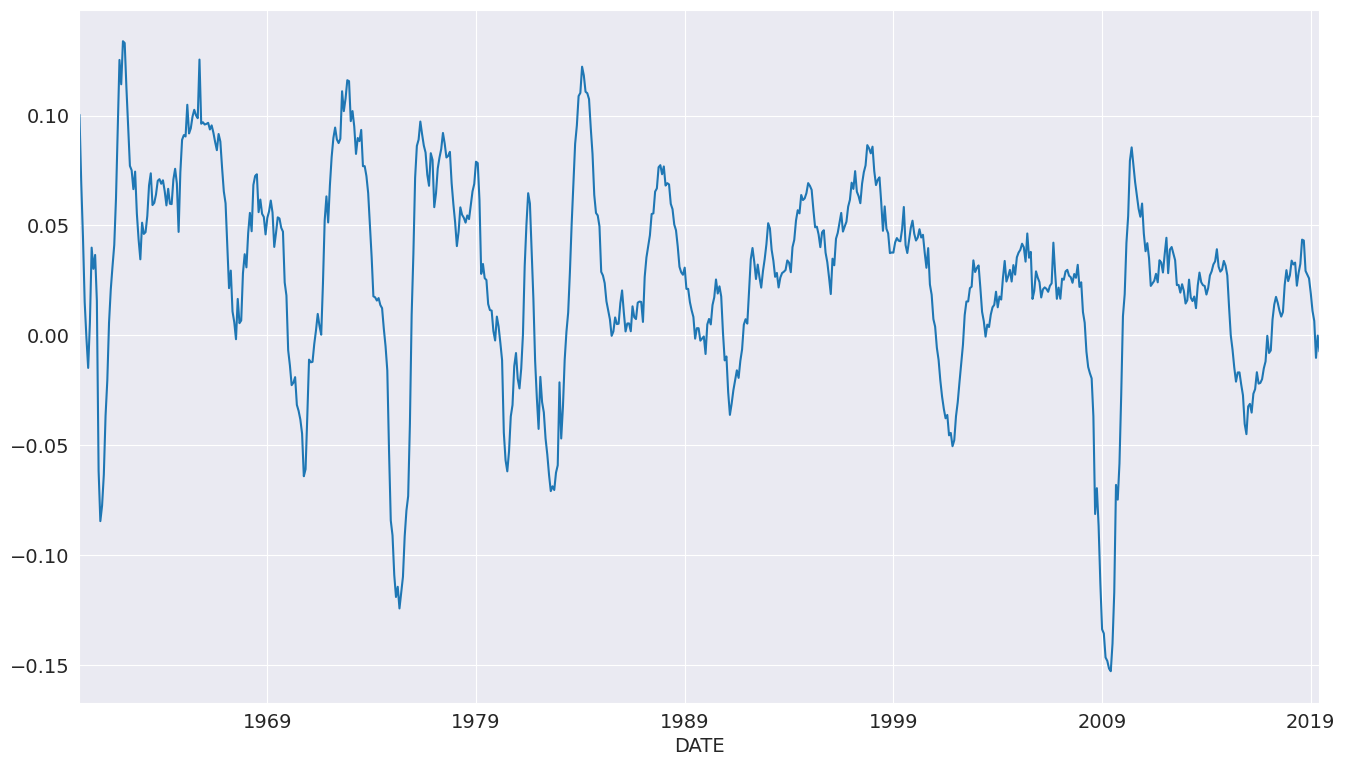
We will start by selecting a model using up to 12 lags. An AR(13) minimizes the BIC criteria even though many coefficients are insignificant.
[18]:
sel = ar_select_order(ind_prod, 13, "bic", old_names=False)
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: AutoReg(13) Log Likelihood 2321.382
Method: Conditional MLE S.D. of innovations 0.009
Date: Thu, 03 Oct 2024 AIC -4612.763
Time: 16:08:12 BIC -4544.476
Sample: 02-01-1961 HQIC -4586.368
- 06-01-2019
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.783 0.005 0.000 0.002
INDPRO.L1 1.1577 0.035 33.179 0.000 1.089 1.226
INDPRO.L2 -0.0822 0.053 -1.543 0.123 -0.187 0.022
INDPRO.L3 7.041e-05 0.053 0.001 0.999 -0.104 0.104
INDPRO.L4 0.0076 0.053 0.143 0.886 -0.096 0.111
INDPRO.L5 -0.1329 0.053 -2.529 0.011 -0.236 -0.030
INDPRO.L6 -0.0080 0.052 -0.153 0.879 -0.111 0.095
INDPRO.L7 0.0556 0.052 1.064 0.287 -0.047 0.158
INDPRO.L8 -0.0296 0.052 -0.568 0.570 -0.132 0.073
INDPRO.L9 0.0920 0.052 1.770 0.077 -0.010 0.194
INDPRO.L10 -0.0808 0.052 -1.552 0.121 -0.183 0.021
INDPRO.L11 -0.0003 0.052 -0.005 0.996 -0.102 0.102
INDPRO.L12 -0.3820 0.052 -7.364 0.000 -0.484 -0.280
INDPRO.L13 0.3613 0.033 10.996 0.000 0.297 0.426
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0408 -0.2913j 1.0808 -0.4566
AR.2 -1.0408 +0.2913j 1.0808 0.4566
AR.3 -0.7803 -0.8039j 1.1204 -0.3726
AR.4 -0.7803 +0.8039j 1.1204 0.3726
AR.5 -0.2728 -1.0533j 1.0880 -0.2903
AR.6 -0.2728 +1.0533j 1.0880 0.2903
AR.7 0.2716 -1.0507j 1.0852 -0.2097
AR.8 0.2716 +1.0507j 1.0852 0.2097
AR.9 0.8010 -0.7285j 1.0827 -0.1175
AR.10 0.8010 +0.7285j 1.0827 0.1175
AR.11 1.0219 -0.2219j 1.0457 -0.0340
AR.12 1.0219 +0.2219j 1.0457 0.0340
AR.13 1.0560 -0.0000j 1.0560 -0.0000
------------------------------------------------------------------------------
We can also use a global search which allows longer lags to enter if needed without requiring the shorter lags. Here we see many lags dropped. The model indicates there may be some seasonality in the data.
[19]:
sel = ar_select_order(ind_prod, 13, "bic", glob=True, old_names=False)
sel.ar_lags
res_glob = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: AutoReg(13) Log Likelihood 2321.382
Method: Conditional MLE S.D. of innovations 0.009
Date: Thu, 03 Oct 2024 AIC -4612.763
Time: 16:08:14 BIC -4544.476
Sample: 02-01-1961 HQIC -4586.368
- 06-01-2019
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.783 0.005 0.000 0.002
INDPRO.L1 1.1577 0.035 33.179 0.000 1.089 1.226
INDPRO.L2 -0.0822 0.053 -1.543 0.123 -0.187 0.022
INDPRO.L3 7.041e-05 0.053 0.001 0.999 -0.104 0.104
INDPRO.L4 0.0076 0.053 0.143 0.886 -0.096 0.111
INDPRO.L5 -0.1329 0.053 -2.529 0.011 -0.236 -0.030
INDPRO.L6 -0.0080 0.052 -0.153 0.879 -0.111 0.095
INDPRO.L7 0.0556 0.052 1.064 0.287 -0.047 0.158
INDPRO.L8 -0.0296 0.052 -0.568 0.570 -0.132 0.073
INDPRO.L9 0.0920 0.052 1.770 0.077 -0.010 0.194
INDPRO.L10 -0.0808 0.052 -1.552 0.121 -0.183 0.021
INDPRO.L11 -0.0003 0.052 -0.005 0.996 -0.102 0.102
INDPRO.L12 -0.3820 0.052 -7.364 0.000 -0.484 -0.280
INDPRO.L13 0.3613 0.033 10.996 0.000 0.297 0.426
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0408 -0.2913j 1.0808 -0.4566
AR.2 -1.0408 +0.2913j 1.0808 0.4566
AR.3 -0.7803 -0.8039j 1.1204 -0.3726
AR.4 -0.7803 +0.8039j 1.1204 0.3726
AR.5 -0.2728 -1.0533j 1.0880 -0.2903
AR.6 -0.2728 +1.0533j 1.0880 0.2903
AR.7 0.2716 -1.0507j 1.0852 -0.2097
AR.8 0.2716 +1.0507j 1.0852 0.2097
AR.9 0.8010 -0.7285j 1.0827 -0.1175
AR.10 0.8010 +0.7285j 1.0827 0.1175
AR.11 1.0219 -0.2219j 1.0457 -0.0340
AR.12 1.0219 +0.2219j 1.0457 0.0340
AR.13 1.0560 -0.0000j 1.0560 -0.0000
------------------------------------------------------------------------------
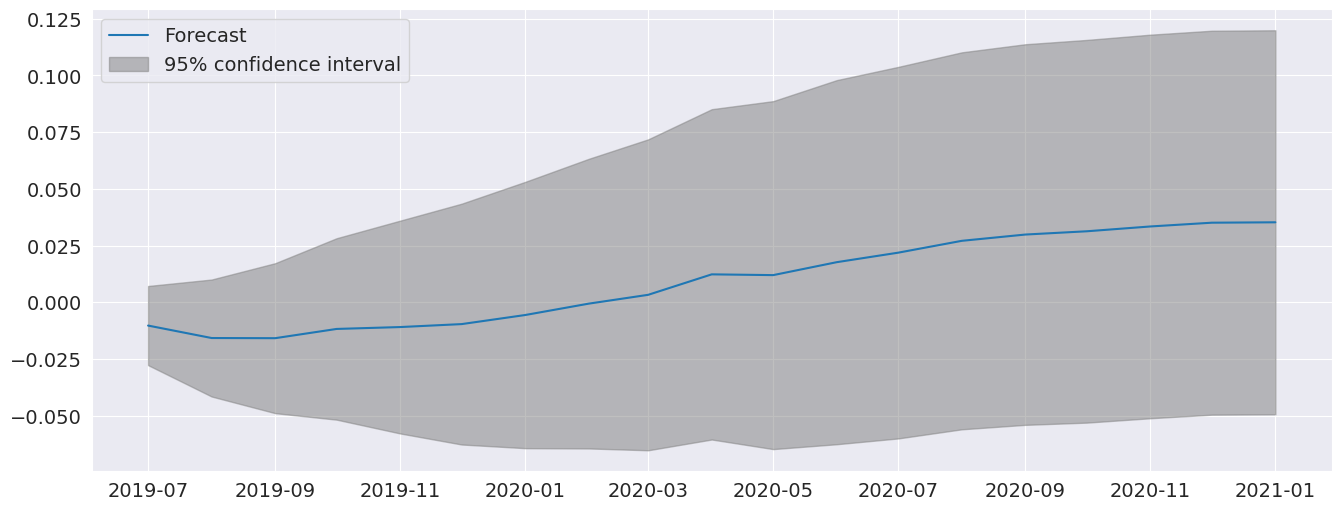
plot_predict can be used to produce forecast plots along with confidence intervals. Here we produce forecasts starting at the last observation and continuing for 18 months.
[20]:
ind_prod.shape
[20]:
(714,)
[21]:
fig = res_glob.plot_predict(start=714, end=732)
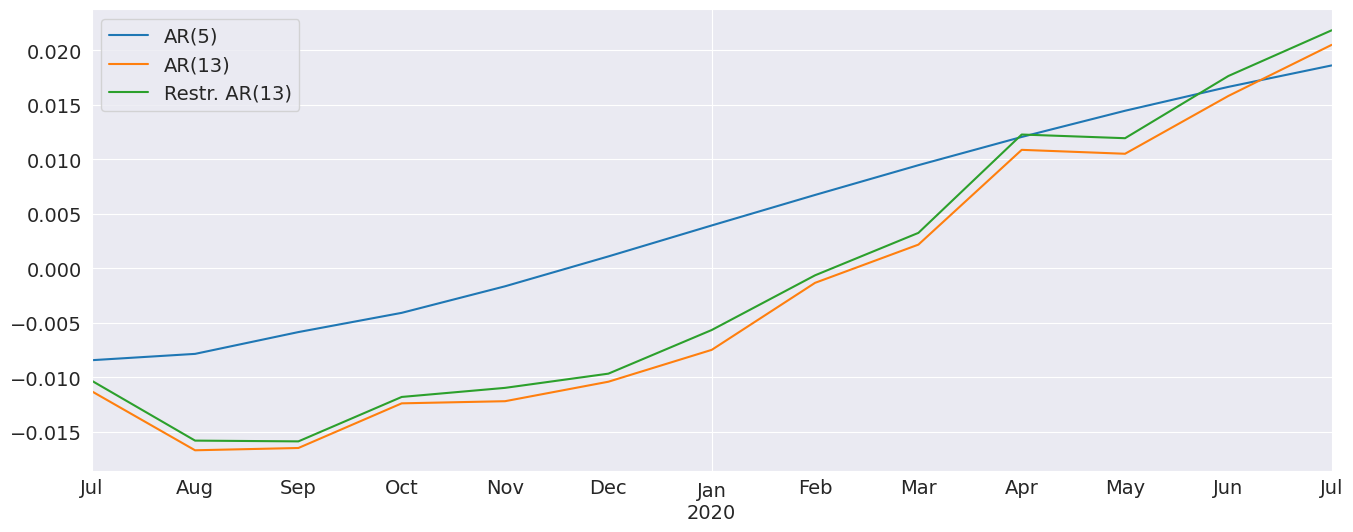
The forecasts from the full model and the restricted model are very similar. I also include an AR(5) which has very different dynamics
[22]:
res_ar5 = AutoReg(ind_prod, 5, old_names=False).fit()
predictions = pd.DataFrame(
{
"AR(5)": res_ar5.predict(start=714, end=726),
"AR(13)": res.predict(start=714, end=726),
"Restr. AR(13)": res_glob.predict(start=714, end=726),
}
)
_, ax = plt.subplots()
ax = predictions.plot(ax=ax)
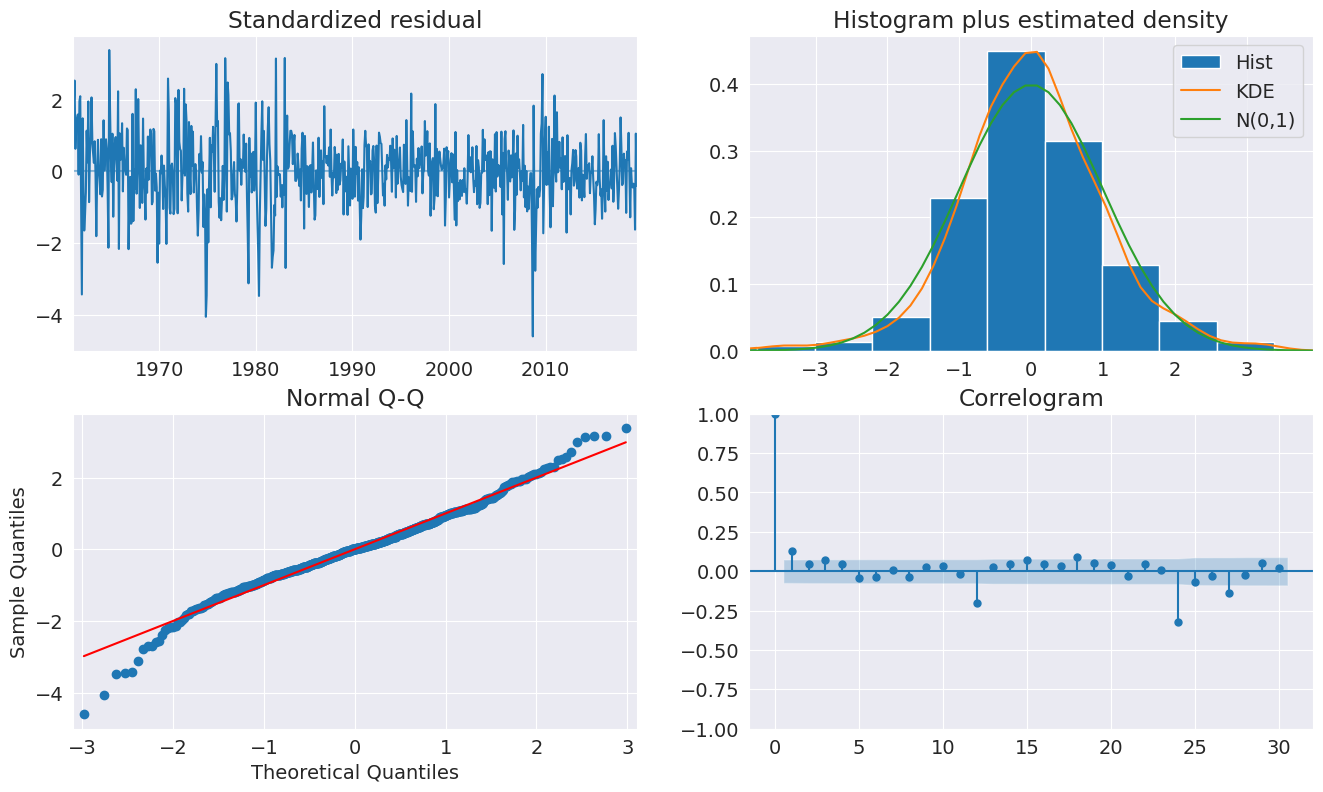
The diagnostics indicate the model captures most of the the dynamics in the data. The ACF shows a patters at the seasonal frequency and so a more complete seasonal model (SARIMAX) may be needed.
[23]:
fig = plt.figure(figsize=(16, 9))
fig = res_glob.plot_diagnostics(fig=fig, lags=30)
Forecasting¶
Forecasts are produced using the predict method from a results instance. The default produces static forecasts which are one-step forecasts. Producing multi-step forecasts requires using dynamic=True.
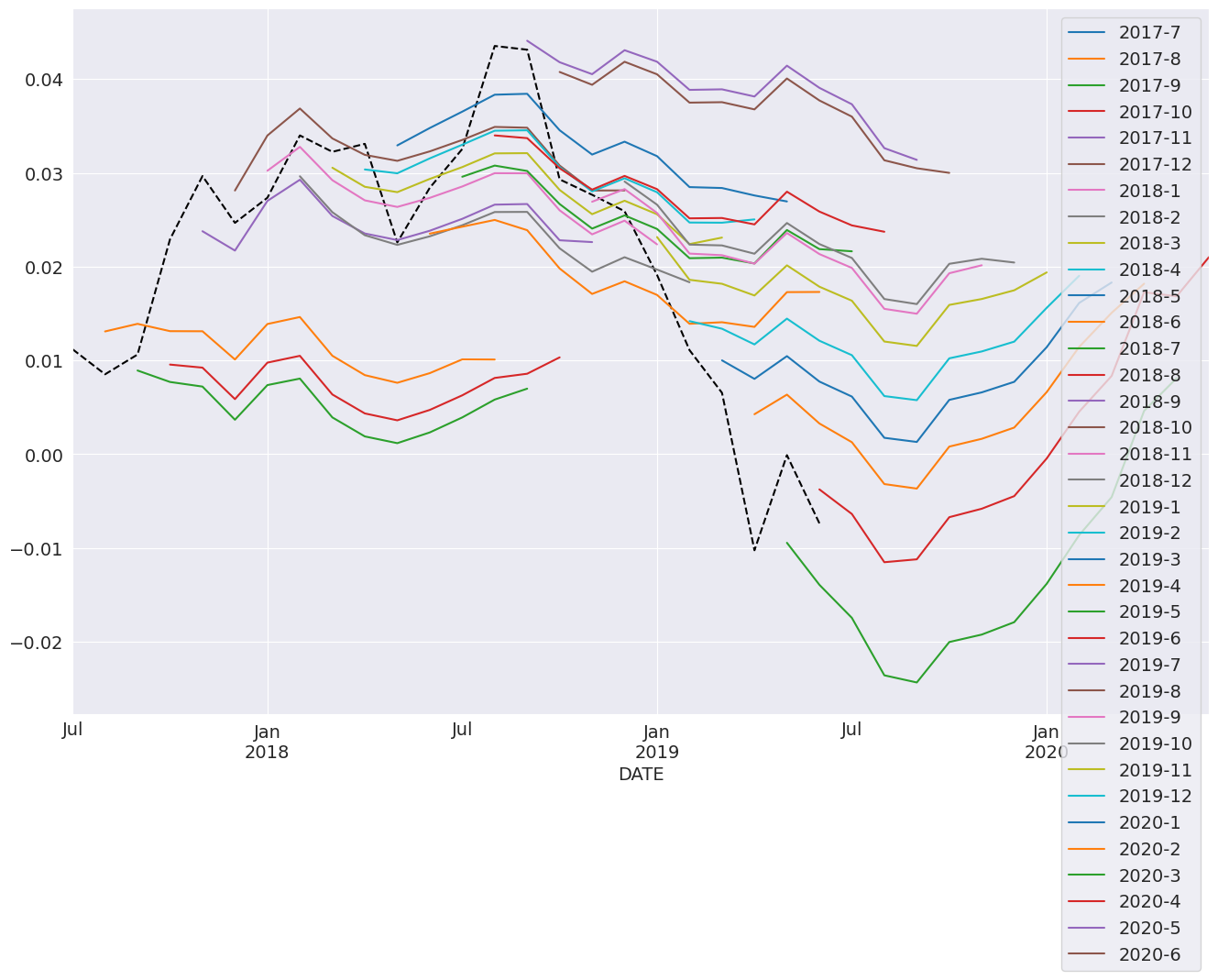
In this next cell, we produce 12-step-heard forecasts for the final 24 periods in the sample. This requires a loop.
Note: These are technically in-sample since the data we are forecasting was used to estimate parameters. Producing OOS forecasts requires two models. The first must exclude the OOS period. The second uses the predict method from the full-sample model with the parameters from the shorter sample model that excluded the OOS period.
[24]:
import numpy as np
start = ind_prod.index[-24]
forecast_index = pd.date_range(start, freq=ind_prod.index.freq, periods=36)
cols = ["-".join(str(val) for val in (idx.year, idx.month)) for idx in forecast_index]
forecasts = pd.DataFrame(index=forecast_index, columns=cols)
for i in range(1, 24):
fcast = res_glob.predict(
start=forecast_index[i], end=forecast_index[i + 12], dynamic=True
)
forecasts.loc[fcast.index, cols[i]] = fcast
_, ax = plt.subplots(figsize=(16, 10))
ind_prod.iloc[-24:].plot(ax=ax, color="black", linestyle="--")
ax = forecasts.plot(ax=ax)
Comparing to SARIMAX¶
SARIMAX is an implementation of a Seasonal Autoregressive Integrated Moving Average with eXogenous regressors model. It supports:
Specification of seasonal and nonseasonal AR and MA components
Inclusion of Exogenous variables
Full maximum-likelihood estimation using the Kalman Filter
This model is more feature rich than AutoReg. Unlike SARIMAX, AutoReg estimates parameters using OLS. This is faster and the problem is globally convex, and so there are no issues with local minima. The closed-form estimator and its performance are the key advantages of AutoReg over SARIMAX when comparing AR(P) models. AutoReg also support seasonal dummies, which can be used with SARIMAX if the user includes them as exogenous regressors.
[25]:
from statsmodels.tsa.api import SARIMAX
sarimax_mod = SARIMAX(ind_prod, order=((1, 5, 12, 13), 0, 0), trend="c")
sarimax_res = sarimax_mod.fit()
print(sarimax_res.summary())
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 6 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= -3.21907D+00 |proj g|= 1.78480D+01
This problem is unconstrained.
At iterate 5 f= -3.22490D+00 |proj g|= 1.52242D-01
At iterate 10 f= -3.22526D+00 |proj g|= 1.46006D+00
At iterate 15 f= -3.22550D+00 |proj g|= 7.46711D-01
At iterate 20 f= -3.22610D+00 |proj g|= 2.52890D-01
At iterate 25 f= -3.22611D+00 |proj g|= 1.80088D-01
At iterate 30 f= -3.22646D+00 |proj g|= 1.46895D+00
At iterate 35 f= -3.22677D+00 |proj g|= 1.05336D-01
At iterate 40 f= -3.22678D+00 |proj g|= 3.20093D-02
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
6 41 64 1 0 0 3.201D-02 -3.227D+00
F = -3.2267786140514940
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
SARIMAX Results
=========================================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: SARIMAX([1, 5, 12, 13], 0, 0) Log Likelihood 2303.920
Date: Thu, 03 Oct 2024 AIC -4595.840
Time: 16:08:18 BIC -4568.415
Sample: 01-01-1960 HQIC -4585.248
- 06-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0011 0.000 2.534 0.011 0.000 0.002
ar.L1 1.0801 0.010 107.331 0.000 1.060 1.100
ar.L5 -0.0847 0.011 -7.592 0.000 -0.107 -0.063
ar.L12 -0.4428 0.026 -17.302 0.000 -0.493 -0.393
ar.L13 0.4073 0.025 16.213 0.000 0.358 0.457
sigma2 9.136e-05 3.08e-06 29.630 0.000 8.53e-05 9.74e-05
===================================================================================
Ljung-Box (L1) (Q): 21.77 Jarque-Bera (JB): 959.65
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 0.37 Skew: -0.63
Prob(H) (two-sided): 0.00 Kurtosis: 8.54
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Warning: more than 10 function and gradient
evaluations in the last line search. Termination
may possibly be caused by a bad search direction.
[26]:
sarimax_params = sarimax_res.params.iloc[:-1].copy()
sarimax_params.index = res_glob.params.index
params = pd.concat([res_glob.params, sarimax_params], axis=1, sort=False)
params.columns = ["AutoReg", "SARIMAX"]
params
[26]:
| AutoReg | SARIMAX | |
|---|---|---|
| const | 0.001234 | 0.001085 |
| INDPRO.L1 | 1.088761 | 1.080116 |
| INDPRO.L5 | -0.105665 | -0.084738 |
| INDPRO.L12 | -0.388374 | -0.442793 |
| INDPRO.L13 | 0.362319 | 0.407338 |
Custom Deterministic Processes¶
The deterministic parameter allows a custom DeterministicProcess to be used. This allows for more complex deterministic terms to be constructed, for example one that includes seasonal components with two periods, or, as the next example shows, one that uses a Fourier series rather than seasonal dummies.
[27]:
from statsmodels.tsa.deterministic import DeterministicProcess
dp = DeterministicProcess(housing.index, constant=True, period=12, fourier=2)
mod = AutoReg(housing, 2, trend="n", seasonal=False, deterministic=dp)
res = mod.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(2) Log Likelihood -2716.505
Method: Conditional MLE S.D. of innovations 10.364
Date: Thu, 03 Oct 2024 AIC 5449.010
Time: 16:08:18 BIC 5485.677
Sample: 04-01-1959 HQIC 5463.163
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.7550 0.391 4.485 0.000 0.988 2.522
sin(1,12) 16.7443 0.860 19.478 0.000 15.059 18.429
cos(1,12) 4.9409 0.588 8.409 0.000 3.789 6.093
sin(2,12) 12.9364 0.619 20.889 0.000 11.723 14.150
cos(2,12) -0.4738 0.754 -0.628 0.530 -1.952 1.004
HOUSTNSA.L1 -0.3905 0.037 -10.664 0.000 -0.462 -0.319
HOUSTNSA.L2 -0.1746 0.037 -4.769 0.000 -0.246 -0.103
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.1182 -2.1159j 2.3932 -0.3274
AR.2 -1.1182 +2.1159j 2.3932 0.3274
-----------------------------------------------------------------------------
[28]:
fig = res.plot_predict(720, 840)
