VARMAX models¶
This is a brief introduction notebook to VARMAX models in statsmodels. The VARMAX model is generically specified as:
\[y_t = \nu + A_1 y_{t-1} + \dots + A_p y_{t-p} + B x_t + \epsilon_t +
M_1 \epsilon_{t-1} + \dots M_q \epsilon_{t-q}\]
where \(y_t\) is a \(\text{k_endog} \times 1\) vector.
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
[3]:
dta = sm.datasets.webuse('lutkepohl2', 'https://www.stata-press.com/data/r12/')
dta.index = dta.qtr
dta.index.freq = dta.index.inferred_freq
endog = dta.loc['1960-04-01':'1978-10-01', ['dln_inv', 'dln_inc', 'dln_consump']]
Model specification¶
The VARMAX class in statsmodels allows estimation of VAR, VMA, and VARMA models (through the order argument), optionally with a constant term (via the trend argument). Exogenous regressors may also be included (as usual in statsmodels, by the exog argument), and in this way a time trend may be added. Finally, the class allows measurement error (via the measurement_error argument) and allows specifying either a diagonal or unstructured innovation covariance matrix (via the
error_cov_type argument).
Example 1: VAR¶
Below is a simple VARX(2) model in two endogenous variables and an exogenous series, but no constant term. Notice that we needed to allow for more iterations than the default (which is maxiter=50) in order for the likelihood estimation to converge. This is not unusual in VAR models which have to estimate a large number of parameters, often on a relatively small number of time series: this model, for example, estimates 27 parameters off of 75 observations of 3 variables.
[4]:
exog = endog['dln_consump']
mod = sm.tsa.VARMAX(endog[['dln_inv', 'dln_inc']], order=(2,0), trend='n', exog=exog)
res = mod.fit(maxiter=1000, disp=False)
print(res.summary())
Statespace Model Results
==================================================================================
Dep. Variable: ['dln_inv', 'dln_inc'] No. Observations: 75
Model: VARX(2) Log Likelihood 361.037
Date: Thu, 14 Dec 2023 AIC -696.074
Time: 14:41:53 BIC -665.946
Sample: 04-01-1960 HQIC -684.044
- 10-01-1978
Covariance Type: opg
===================================================================================
Ljung-Box (L1) (Q): 0.04, 10.22 Jarque-Bera (JB): 11.10, 2.44
Prob(Q): 0.84, 0.00 Prob(JB): 0.00, 0.30
Heteroskedasticity (H): 0.45, 0.40 Skew: 0.16, -0.38
Prob(H) (two-sided): 0.05, 0.03 Kurtosis: 4.86, 3.44
Results for equation dln_inv
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
L1.dln_inv -0.2424 0.093 -2.618 0.009 -0.424 -0.061
L1.dln_inc 0.2827 0.448 0.631 0.528 -0.595 1.161
L2.dln_inv -0.1621 0.155 -1.045 0.296 -0.466 0.142
L2.dln_inc 0.0816 0.421 0.194 0.846 -0.744 0.907
beta.dln_consump 0.9634 0.637 1.513 0.130 -0.285 2.212
Results for equation dln_inc
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
L1.dln_inv 0.0622 0.036 1.732 0.083 -0.008 0.133
L1.dln_inc 0.0824 0.107 0.768 0.443 -0.128 0.293
L2.dln_inv 0.0093 0.033 0.282 0.778 -0.055 0.074
L2.dln_inc 0.0328 0.134 0.244 0.807 -0.230 0.296
beta.dln_consump 0.7754 0.112 6.905 0.000 0.555 0.995
Error covariance matrix
============================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------------
sqrt.var.dln_inv 0.0433 0.004 12.327 0.000 0.036 0.050
sqrt.cov.dln_inv.dln_inc 3.564e-05 0.002 0.018 0.986 -0.004 0.004
sqrt.var.dln_inc 0.0109 0.001 11.202 0.000 0.009 0.013
============================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
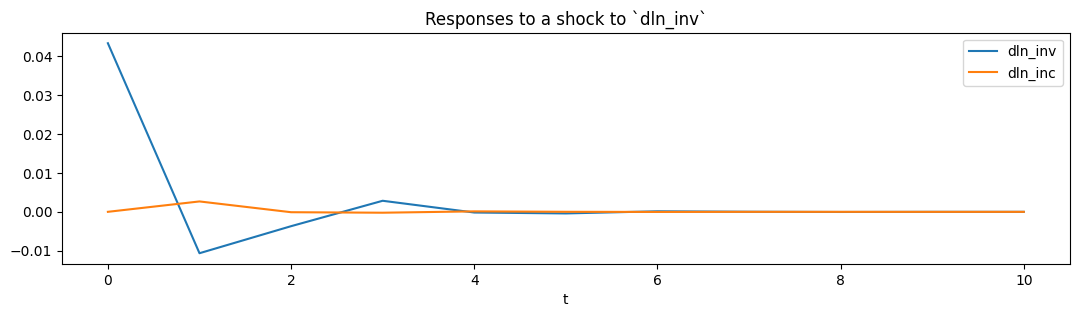
From the estimated VAR model, we can plot the impulse response functions of the endogenous variables.
[5]:
ax = res.impulse_responses(10, orthogonalized=True, impulse=[1, 0]).plot(figsize=(13,3))
ax.set(xlabel='t', title='Responses to a shock to `dln_inv`');
Example 2: VMA¶
A vector moving average model can also be formulated. Below we show a VMA(2) on the same data, but where the innovations to the process are uncorrelated. In this example we leave out the exogenous regressor but now include the constant term.
[6]:
mod = sm.tsa.VARMAX(endog[['dln_inv', 'dln_inc']], order=(0,2), error_cov_type='diagonal')
res = mod.fit(maxiter=1000, disp=False)
print(res.summary())
Statespace Model Results
==================================================================================
Dep. Variable: ['dln_inv', 'dln_inc'] No. Observations: 75
Model: VMA(2) Log Likelihood 353.888
+ intercept AIC -683.776
Date: Thu, 14 Dec 2023 BIC -655.966
Time: 14:42:10 HQIC -672.672
Sample: 04-01-1960
- 10-01-1978
Covariance Type: opg
===================================================================================
Ljung-Box (L1) (Q): 0.00, 0.05 Jarque-Bera (JB): 12.58, 13.55
Prob(Q): 0.95, 0.82 Prob(JB): 0.00, 0.00
Heteroskedasticity (H): 0.44, 0.81 Skew: 0.05, -0.48
Prob(H) (two-sided): 0.04, 0.60 Kurtosis: 5.00, 4.84
Results for equation dln_inv
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
intercept 0.0182 0.005 3.802 0.000 0.009 0.028
L1.e(dln_inv) -0.2593 0.106 -2.454 0.014 -0.466 -0.052
L1.e(dln_inc) 0.5277 0.631 0.836 0.403 -0.709 1.764
L2.e(dln_inv) 0.0311 0.149 0.209 0.834 -0.261 0.323
L2.e(dln_inc) 0.1759 0.476 0.369 0.712 -0.757 1.109
Results for equation dln_inc
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
intercept 0.0207 0.002 13.058 0.000 0.018 0.024
L1.e(dln_inv) 0.0482 0.042 1.159 0.246 -0.033 0.130
L1.e(dln_inc) -0.0745 0.140 -0.533 0.594 -0.348 0.200
L2.e(dln_inv) 0.0178 0.042 0.419 0.675 -0.065 0.101
L2.e(dln_inc) 0.1257 0.153 0.823 0.411 -0.174 0.425
Error covariance matrix
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
sigma2.dln_inv 0.0020 0.000 7.349 0.000 0.001 0.003
sigma2.dln_inc 0.0001 2.33e-05 5.828 0.000 9e-05 0.000
==================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Caution: VARMA(p,q) specifications¶
Although the model allows estimating VARMA(p,q) specifications, these models are not identified without additional restrictions on the representation matrices, which are not built-in. For this reason, it is recommended that the user proceed with error (and indeed a warning is issued when these models are specified). Nonetheless, they may in some circumstances provide useful information.
[7]:
mod = sm.tsa.VARMAX(endog[['dln_inv', 'dln_inc']], order=(1,1))
res = mod.fit(maxiter=1000, disp=False)
print(res.summary())
/opt/hostedtoolcache/Python/3.10.13/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/varmax.py:161: EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
warn('Estimation of VARMA(p,q) models is not generically robust,'
Statespace Model Results
==================================================================================
Dep. Variable: ['dln_inv', 'dln_inc'] No. Observations: 75
Model: VARMA(1,1) Log Likelihood 354.292
+ intercept AIC -682.585
Date: Thu, 14 Dec 2023 BIC -652.458
Time: 14:42:19 HQIC -670.555
Sample: 04-01-1960
- 10-01-1978
Covariance Type: opg
===================================================================================
Ljung-Box (L1) (Q): 0.00, 0.04 Jarque-Bera (JB): 11.27, 13.92
Prob(Q): 0.96, 0.84 Prob(JB): 0.00, 0.00
Heteroskedasticity (H): 0.43, 0.91 Skew: 0.01, -0.45
Prob(H) (two-sided): 0.04, 0.81 Kurtosis: 4.90, 4.91
Results for equation dln_inv
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
intercept 0.0105 0.067 0.156 0.876 -0.121 0.142
L1.dln_inv -0.0001 0.724 -0.000 1.000 -1.420 1.419
L1.dln_inc 0.3753 2.819 0.133 0.894 -5.149 5.900
L1.e(dln_inv) -0.2513 0.734 -0.342 0.732 -1.690 1.188
L1.e(dln_inc) 0.1206 3.069 0.039 0.969 -5.894 6.135
Results for equation dln_inc
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
intercept 0.0164 0.028 0.583 0.560 -0.039 0.071
L1.dln_inv -0.0334 0.289 -0.116 0.908 -0.601 0.534
L1.dln_inc 0.2389 1.139 0.210 0.834 -1.993 2.471
L1.e(dln_inv) 0.0891 0.296 0.300 0.764 -0.492 0.670
L1.e(dln_inc) -0.2454 1.174 -0.209 0.834 -2.546 2.055
Error covariance matrix
============================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------------
sqrt.var.dln_inv 0.0449 0.003 14.510 0.000 0.039 0.051
sqrt.cov.dln_inv.dln_inc 0.0017 0.003 0.650 0.515 -0.003 0.007
sqrt.var.dln_inc 0.0116 0.001 11.723 0.000 0.010 0.013
============================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Last update:
Dec 14, 2023